> restart;

Math B14-1

Some Max Min Word Problems

Example 1. The volume of 1 kg of water at temperature is given by

Find the temperature of maximum density.

Solution . The density at temperature is mass (1kg) divided by volume, so it is the reciprocal of the above expression. Denoting the density by , we make the Maple definition

> f:= T ->
1/(999.87 -(0.06426)*T + (0.0085043)*T^2 -(0.0000679)*T^3);

We want to plot the function to get an idea of what the graph looks like. We know must be non-negative, and we pick some reasonably large value of for an upper limit, say .

> plot(f(T),T=0..30);

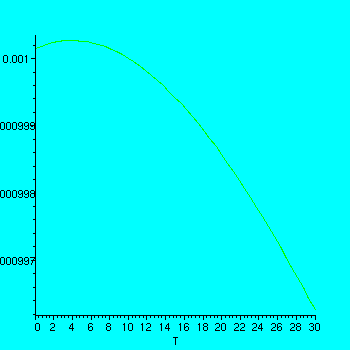
Use Maple to find

> limit(f(T),T=infinity);

So we can be reasonably sure the maxium occurs within the interval we have chosen.

>

Now use calculus to find the absolute maximum of on the interval . In Maple we find the derivative with the D operator, that is, D(f) is the function obtained by differentiating the function f and is the value of the derivative at .

> D(f);

Using Maple to compute the derivative for us saves us a lot of time doing algebra. Now plot the derivative function to get some idea where it is zero.

> plot(D(f)(T), T= 0..30);

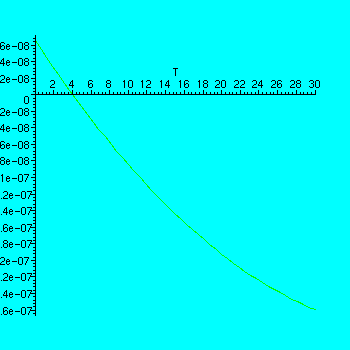
It appears there is a root somewhere near . But we can just ask Maple to find this

root for us by using.

> solve(D(f)(T) = 0,T);

Note that this actually gave two solutions, but one of them is not within the interval under consideration. The only candidates for the maximum in the given interval are the first root given above or the endpoints of the interval. However, it is clear from the graph of that the maximum occurs at the internal point where the derivative vanishes.

But just to be sure let's evaluate f(T) at the three values of T which are possible candidates..

> f(0); f(3.96651463); f(30);

We see that the second value is the largest, being slightly larger than the first value and not too much larger than the third value.

>

Now we solve another word problem in which the quantity to be optimized initially involves two variables but where there is a relation between the variables.

Example 2, A printed page must contain of printed material. There are to be margins of 5 cm on either side and margins of 3 cm on the top and bottom. What should the dimensions and of the total page be in order to minimize the amount of paper used?

Hint .

Solution . First we derive a formula for the function which describes the area of the rectangle: You should draw a picture of the page so you can follow the steps in the algebra below.

> A := x*y;

But there is a relation among the variables as indicated in the hint since the page must contain 60 of printed material. We ask Maple to solve the equation in the hint for in terms of .

> expression := solve((x-10)*(y - 6) = 60,y);

Now substitute this value of y in the formula for and use that to form a function only of . We have to use the Maple command unapply , but don't worry about the form of the command. Note however that it produces a function of .

> g := unapply(subs(y=expression,A),x);

Note that the appropriate interval to look at is , since the page cannot be narrower than 10 cm. (Each margin is 5 cm.)

Now find the internal critical point(s) by setting the derivative equal to zero.

> D(g);
solve(D(g)(x)=0,x);

Clearly, is the desired solution, if there is one, since is outside the domain of the function. But can we be sure this problem has a solution at all? To see that it does, let's plot the function over an appropriate range. Since there was no upper limit on either dimension, the appropriate interval to draw the graph 0 to .

> plot(g(x),x=10..infinity);

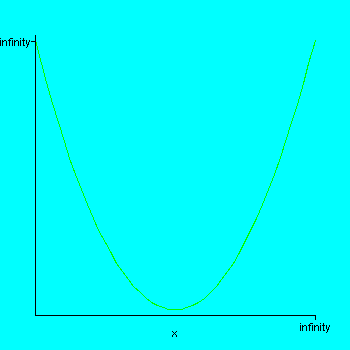
Note that the function does in fact have an absolute minimum. (But don't take too seriously Maple's claim that it has actually graphed the function out to infinity.) So we must have found the absolute minimum for . To find the corresponding value of , substitute in the expression for .

> subs(x=20,expression);

>

Homework

Try doing exactly the same problem, but wiith the assumption that both vertical and horizontal margins are 5 cm. Thus, in the relation between and , you should replace `y-6' by `y - 10'. You may either go back and change the appropriate entries in both the commands and the text, or if you are ambitious, you may try to copy it all below by copying and pasting, and change it there. You will discover that the correct value of involves a square root. To evaluate the corresponding value of you will have to put this value of in the subs command. This will require you to use the Maple function command sqrt(a) for . Put the values you obtained for and below. To get a decimal approximation to , apply the Maple command evalf by putting it before the subs command and enclosing all of the latter in parentheses.