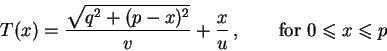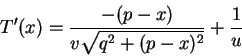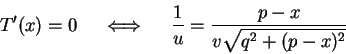The Fastest Route

The Fastest Route

Problem:

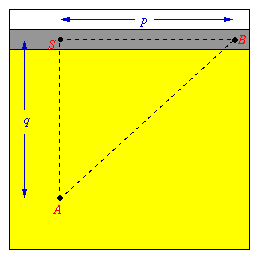
Suppose you are in the middle of a desert ( point A ) and you want to get to the town ( point B ) as fast as possible. Of course you can go straight from A to B, but you cannot move too fast in the desert. Going to the road first ( point S ) and hitching a ride there might be a better choice. So here is the problem: How to choose point S so as to minimize the time T it takes to get from A to B?

Solution:
The town B is q miles north and p miles east from A. You can go v mph on the desert and u mph on the road ( v<u ). Let x be the distance from S to B. You can change the position of A and S by "dragging" them with the mouse or by changing p, q or x. On the right you can see a graph of the time T with respect to x. Clicking on "Optimize" will give you the best location of S.

Now let us solve the problem. We can express the time T as

$\begin{displaymath}T=\frac{\vert AS\vert}{v}+\frac{\vert SB\vert}{u} \end{displaymath}$

where |AS| is the distance from A to S in miles and |SB| is the distance from S to B. It is easy to see that

$\begin{displaymath}\vert AS\vert=\sqrt{q^2+(p-x)^2}\qquad\mbox{and}\qquad \vert SB\vert=x \end{displaymath}$

So finally

$\begin{displaymath}T(x)=\frac{\sqrt{q^2+(p-x)^2}}{v}+\frac{x}{u}\,,\qquad \mbox{for }0\leqslant x\leqslant p \end{displaymath}$

Our task is to find the absolute minimum of T(x) on [0,p]. First we will find all critical points of T.

$\begin{displaymath}T^\prime(x)=\frac{-(p-x)}{v\sqrt{q^2+(p-x)^2}}+\frac{1}{u} \end{displaymath}$

$\begin{displaymath}T^\prime(x)=0\quad\iff\quad \frac{1}{u}=\frac{p-x}{v\sqrt{q^2+(p-x)^2}} \end{displaymath}$

$\begin{displaymath}x_0=p-\frac{vq}{\sqrt{u^2-v^2}} \end{displaymath}$

So now all we have to do is to test the value of T at 0, p and at x₀ ( provided that 0<x₀<p - sometimes T(x) has a local extremum outside [0,p] ).