Around 500 BC, there was a Greek philosopher named Zeno. You've probably heard of him, or at least of the dilemma he raised. He stated it in a number of different ways, but I shall concentrate on just one.
The hero, Achilles, and the tortoise agree to a foot race. The tortoise complains that Achilles has the gift of speed, but alas he, the tortoise, does not. So he petitions Achilles for a handicap. And Achilles agrees to allow the tortoise a 1000 meter head start. Surely, Achilles thinks to himself, I can still win this race.
Now Achilles certainly does have the gift of speed and can do a steady 5 meters per second without even breaking a sweat. So that is how fast Achilles decides to run. But the poor tortoise redlines at just half a meter per second. And knowing that he'll have to do his very best even to have a chance against the speedster, Achilles, he must go just as fast has he can go.
The starting signal sounds precisely at noon. The problem is to figure out exactly what time Achilles passes the tortoise.
Well, a little elementary algebra quickly gives us an answer. If xA is where Achilles is, xT is where the tortoise is, and t is seconds past noon, we have the following equations:
/ 1 meters \
xT = 1000 meters + ( - ------ * t ) equation of the tortoise
\ 2 second /
eq. 2.0-1
/ meters \
xA = 0 meters + ( 5 ------ * t ) equation of Achilles
\ second /
Since Achilles and the tortoise must be in exactly the same spot when one passes the other, we solve for xA = xT. This being the case, we can subtract the two equations above to get:
/ 1 meters \
0 = 1000 meters - ( 4- ------ * t ) eq 2.0-2
\ 2 second /
2
t = 222 - seconds
9
Zeno probably also had the algebraic wherewithall to solve the problem in a similar way. But he observed that after 200 seconds, Achilles runs the 1000 meter distance of the tortoise's head start. At that time he is where the tortoise started. But in that amount of time, the tortoise has run 100 meters. So 20 seconds later (that is at t = 220 seconds) Achilles catches up to that spot. But in those 20 seconds, the tortoise has run another 10 meters. It takes Achilles only 2 seconds to catch up to that spot. But by then, the tortoise has run another meter. Zeno realized that this process goes on forever, with Achilles always catching up to where the tortoise was, and the tortoise always running a little bit farther. So how can Achilles ever pass the tortoise?
We actually have several examples of things that tend to a limit in this parable. We have the sequence of times, t1, t2, t3, etc. At each tj Achilles is where the tortoise was at tj-1. That defines all the tj's except t1, which we will say is the moment of the starting signal. So the various tj's are:
t1 = 0 seconds eq. 2.0-3
t2 = 200 seconds
t3 = 220 seconds
t4 = 222 seconds
t5 = 222.2 seconds
t6 = 222.22 seconds
.
.
.
I'm sure you can see the pattern here, but can you prove it? Yes, you can, and you're going to do so right now.
(Think back to how you solved rate
problems in algebra. Remember that
By what factor does Achilles' speed exceed the tortoise's? Get that by dividing the tortoise's speed into Achille's speed. Call that number r for ratio. Now, if it takes the tortoise an amount of time, delta_t, to run some distance, how long does it take Achilles to run that same distance ? Get that by dividing delta_t by r. Why? (refer to the rate formula given above).
Now observe that during each interval, Achilles runs the same distance that the tortoise ran in the previous interval. Here is the pattern of the intervals, which we call delta_t's:
delta_t1 = t2 - t1 = 200 seconds - 0 seconds = 200 seconds delta_t2 = t3 - t2 = 220 seconds - 200 seconds = 20 seconds delta_t3 = t4 - t3 = 222 seconds - 220 seconds = 2 seconds . . . eq. 2.0-4Notice that the delta_t's go down by a factor of 10 each time. Why? Well, you arrived at
We already know that Achilles passes the tortoise at
2
t = 222 - seconds eq. 2.0-5
9
from the algebra we did before. Can we show that the sequence of
tj's has this as its limit? Well, what do we have to show? We
have to show that if I tell you how close you want tj to be to
the t we gave above, then you can tell me how far into the sequence
of tj's I have to go in order to assure me that all the
tj's that
follow are at least that close.
You instructor will word it in a different way. He or she will say,
"given any epsilon greater than zero, you need to be able to
find an n
big enough so that
Don't let the Greek symbol or the mathematical formalism intimidate you. The statement of the problem I gave means precisely the same thing as the one your instructor gives. A limit means simply, I tell you how close I need to be, and you can tell me what I have to do to be that close. In the formal version of this, epsilon is the "how close I gotta be" and n is the "what I gotta do to be that close."
If I say, for example, I've got to be within a thousandth of a second
of t (i.e.
But so far we haven't proved the assertion. To prove it, we must show that we can always find how far to go no matter how close we have to be. Let's do that now.
We can see that the jth term of the sequence given in 2.0-3
is a bunch of 2's, beginning in the hundreds column and extending
rightward. There are always j-1 2's in each decimal. So we can
easily write the decimal for any term in the series. The 13th, for
example, is:
It's pretty clear that after t3 all the tj's are within 1 of 222. So all we will prove is that the fractional part of the sequence (that is the part to the right of the decimal point) converges to a limit of 2/9.
So let's find the difference between a bunch of 2's to the right of the decimal point and 2/9. Recall that if we have n 2's to the right of the decimal point, what we really have is the counting number made of n digits of 2's divided by 10n. So, for example, nine 2's to the right of the decimal point means:
222222222
0.222222222 = --------- eq. 2.0-6
109
So, in the example where n=9, we are interested in:
| 2 222222222 |
epsilon = | - - --------- | eq. 2.0-7
| 9 109 |
epsilon represents how close we are to the limit.
We have to put these fractions over a common denominator in order to subract them. So to the right-hand one we have to multiply top and bottom by 9. To the left-hand one we have to multiply top and bottom by 109. We get:
| 2000000000 1999999998 | 2
epsilon = | ---------- - ---------- | = ---------- eq. 2.0-8
| 9000000000 9000000000 | 9000000000
In fact, when you multiplied those nine 2's by 9, it became
pretty clear that there is a pattern there. And if you multiply n 2's
by 9, what you will always get is a 1 followed by
n-1 9's, followed by an 8. And when you subtract that from
2 * 10n, you will always get 2. So that will
always be the numerator of the difference. And the denominator? Clearly
it will always be 9 * 10n. So for a decimal point
followed by n 2's, we have:
2
epsilon = ----- eq. 2.0-9
9*10n
So, can you make epsilon as close to zero as you like by choosing
the right n? and does epsilon stay at least that close
for all subsequent n? The answer is clearly yes, because the
numerator doesn't change as n gets big, but the denominator keeps
getting more and more huge.
Well we have diverged a long way from the foot race. So what have we proved?
We have proved that the sequence of times, tj, does
indeed converge to a limit, and that limit is the same time that we predicted
earlier, using algebra, that Achilles should be passing the tortoise. We can
tell Mr. Zeno that even if he can never see how Achilles gets to
And since we know that Achilles does indeed pass the tortoise, our notion of a limit bears a true connection to reality. Zeno's dilemma was that the sequence of times leading up to the passing represented a completed infinite, yet the infinite is defined as that which never ends. Zeno's problem was that he had a poor definition of "infinite." Infinites do end all the time. And they end in a limit.
When I was a kid, my aunt went and bought this tiny little car. Undoubtably the real reason she did it was because she was going through some financial difficulties at the time, and it was all she could afford. But what she told her kids (my cousins) was that small cars were good. Big cars hog the road, don't drive well, destroy the earth, and so on. Well one day my aunt and cousins showed up packed into this thing. The eldest of my cousins got out and proceded to repeat the whole "small car good, big car bad," line to me. We then walked down the driveway, and there was our big old station wagon, which my dad had assured me was a great car. So I asked my cousin, "Is this car too big?" Realizing that a little tact was called for, he replied, "No, but if it were any bigger, it would be too big."
Well, I found that response perfectly maddening. You mean, if you added just one inch, it would be too big? What if you just added a coat of paint to the bumper -- that would make it a little bigger. Would it be too big then? It was clear to me that there was no place where too-biggness started, only a place where small-enough ended. What was maddening had nothing to do with my cousin. It had everything to do with discovering something new about how the world works. What was the biggest a car could be and not be too big? Our station wagon filled that bill. But what was the smallest a car could be and still be too big? In my cousin's world, no such thing could possibly exist.
It took days for me to resolve this dilemma in my own head. And what resolved it was thinking about all the little-boy macho games I had played with other boys -- like the time a bunch of us found our way to the roof of a condemned building and dared each other how close to the edge of the roof we could stand. Clearly there was a place where you could not stand, and if you tried to stand there you would find yourself plummeting toward the ground. But there was no place that was the absolute limit of where you could stand without falling, and that, of course, was the whole point of the game. No matter how close you stood to the edge, some other guy could stoke up his courage and skooch just a tad closer to disaster than you were.
And this brings us to another kind of a limit. How close can you stand to mathematical disaster without falling off the edge? But what is mathematical disaster? Well, division by zero, for one. Thou shalt divide by any of the fruits of this garden, but by the tree of zero, thou shalt not divide. You mean I can divide by a tiny little number like 0.00000001, but not by zero? Yep. Even by 0.0000000000001? Yep -- even tinier than that. Just don't go dividing by zero.
So there is that spot we can't stand on without falling. But if I dare you to stand closer to it than I am, you can always do it.
So suppose I had the function:
x2 - 3*x + 2
y = ------------- eq. 2.1-1
x - 1
Well, you can probably quickly convince yourself that the numerator of
2.1-1 factors and you have the same as:
(x - 1) * (x - 2)
y = ----------------- eq. 2.1-2
x - 1
And of course the y = x - 2 eq. 2.1-3Well, kind of. That works for all values of x except
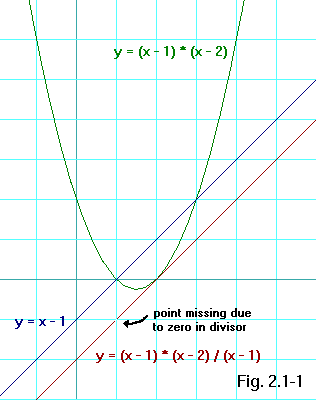 The figure shows the missing point at
The figure shows the missing point at
Let's go back to the macho boys standing on the roof of the condemned building, but imagine that it's a sloped roof. So the altitude of each boy's feet varies according to where on the roof he is standing. Based upon how far right or left a boy is standing, we can determine how high his feet are. Imagine that red trace of our graph represents the roof. The hole in the graph is a hole in the roof. If one of the boys tries to stand there, he will fall all the way to the basement and his mother will be angry with him. But the boys persist in a game of who-can-stand-nearest-the-hole. So how high would a boy's feet be if he could stand on the hole?
In a way, that sounds like an absurd question -- rather like the proverbial tree falling in the woods with nobody around. You could even be a smartass about it and say his feet would be at the same altitude as the rest of him, all twisted up in the basement. Yet we have a sense that there is a serious answer to this based upon the behavior of the rest of the roof.
Let's say we measure altitude from the basement, which on our graph we'll
say is at
We can learn much from the game they are playing. We see that the closer
a boy stands to the hole, the closer his feet are to being exactly
And that's the point. If you can tell me how close the boy's feet have
to be to
lim altitude of his feet = 9 meters
boy's position --> position of hole
Or to put it more traditionally, let x be the boy's position.
Let xh be the position of the hole. Let
af
be the altitude above the basement of his feet. Then we write:
lim af = 9 meters
x --> xh
Now let's analyse equations 2.1-1 and 2.1-2 again. As we already observed,
everywhere except at
(x - 1) * (x - 2)
lim ----------------- = (x - 2) = -1
x --> 1 (x - 1)
It is with near certainty that your teacher will call upon you to prove
this or that limit is equal to such and such. And he or she will want
you to use the traditional method of delta and epsilon
to do it.
Before I demonstrate that for you, I want you to make the connection between
this and what we have been talking about. In the case of the boy on the
roof, I could tell you how close I wanted the altitude of his feet to
be to
In the delta and epsilon proofs, the epsilon is the how close the dependent value has be, and the delta is the how close you have to make the independent variable to the "goes toward" value in order to make that happen.
In the case of the boy on the roof, the epsilon is how close
his feet are to being exactly
In equations 2.1-1 and 2.1-2, the epsilon is how close y is to -1 and the delta is how close x is to 1.
The typical way you see it phrased in a math text is:
We say that:Don't let the formalism intimidate you. What it means is this: You have some real valued function of x, and for convenience we'll call it f(x) (that is it returns some real value for each real value, x in its domain, that you feed it). f(x) could be almost any expression of x you can think of. You want to see if f(x) approaches some value, y, as x approaches some other value, a.lim f(x) = y x --> aif and only if for each epsilon > 0 there exists a delta such that|f(x) - y| < epsilon whenever |x - a| < delta .
The test is, I name how close to y I want f(x) to be. That is I say I want f(x) to be within epsilon of y. If, no matter how small an epsilon I name, you can name how close x has to be to a in order to guarantee what I asked for, then you have proved the limit.
So in the example of equations 2.1-1 and 2.1-2, we have:
(x - 1) * (x - 1)
f(x) = ----------------- eq. 2.1-3
(x - 1)
We also have In general, if you can show a formula that, given an epsilon, turns out a delta that always meets the test, then you have met your teacher's test, and he or she will mark your work correct.
We have discussed two kinds of limits so far, a limit that a sequence of numbers approaches, and a limit that a function approaches. They may seem very different, but they aren't. In both cases, a limit is like a contract. It says, if you need to be this close to something (and it doesn't matter how close this close is), then I can tell you what you need to do to be this close. That is what the delta-epsilon proofs are all about. That is what limits are always about.
The first type of limit is similar to a race-car mechanic telling the machinist how accurately the engine parts must be cut, and the machinist telling him how many dollars it will cost. However accurate the mechanic wants it, the machinist can deliver it with that accuracy. But the tighter the tolerance, the more the cost.
The second is similar to aiming a rifle. You tell the marksman how close to the bullseye he has to hit, and he can tell you how still he has to hold the rifle in order to make that happen.
Here is a graphic that illustrates the delta-epsilon method of
proving the second kind of limit.
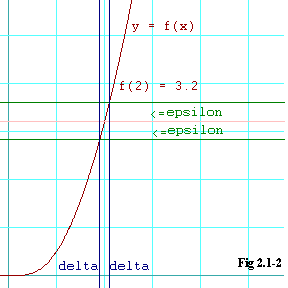 The two green horizontal lines are no more than epsilon above the
limit as
x goes toward 2 and no more than epsilon below
the limit.
The two blue vertical lines are spaced delta on either side of
The two green horizontal lines are no more than epsilon above the
limit as
x goes toward 2 and no more than epsilon below
the limit.
The two blue vertical lines are spaced delta on either side of
If you remember these underlying ideas about limits, learning the details of how to do limits proofs will be a lot easier for you.