Lista XI
Aplicações da Derivada
Soluções

MathBio

Solução do problema 1

Da figura

**Figura 1:** Escada
$\includegraphics[width=0.50\textwidth]{exer1.eps}$

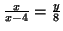podemos escrever: $\frac{x}{x-4}=\frac{y}{8}$ e portanto
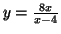$y=\frac{8x}{x-4}$ . A função que descreve o comprimento da escada que pode ser apoiada sobre o muro e alcança o edifício tem como expressão:

$\begin{displaymath}f(x)=d^2=x^2+\left(\frac{x}{x-4}\right)^2.\end{displaymath}$

Derivando obtemos:

$\begin{displaymath}f'(x)=2x+2\left(\frac{x}{x-4}\right)\left(\frac{8(x-4)-8x}{(x-4)^2}\right)= 2x\left(1-\frac{56}{(x-4)^3}\right)\end{displaymath}$

Os zeros da derivada são as soluções de:

$\begin{displaymath}2x\left(1-\frac{56}{(x-4)^3}\right)=0\end{displaymath}$

isto é, x=0 ou x=4(2^2/3+1). Como x varia no intervalo $[4, \infty]$ somente nos interessa a segunda raiz.

$\begin{displaymath}f''(x)=2-\left(\frac{512(x-4)^3-512. 3(x-4)^2}{(x-4)^6}\right) = 2-\left(\frac{512(-2x-4)}{(x-4)^4}\right)\end{displaymath}$

f''(4(2^2/3+1))=3.(2^2/3)+6>0.

indicando que esta raiz é um mínimo. Calculando f nesta raiz obtemos:

$\begin{displaymath}d^2=277.147\qquad d=16,6477\end{displaymath}$

Solução do problema 2 Seja x a variável que representa o comprimento de um lado do retângulo inscrito:

$\begin{displaymath}A_R(x)=x\left(-\frac{3}{4}+3\right)=-\frac{3}{4}x^2+3x\end{displaymath}$

que derivando e igualando a zero dá:

$\begin{displaymath}A_R'(x)=-\frac{3}{2}x+3=0\end{displaymath}$

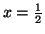isto é $x=\frac{1}{2}$ .

A_R''(x)=-3/2<0

verificando que x=1/2 é um máximo local.

$\begin{displaymath}A_R(1/2)=-\frac{3}{4}(\frac{1}{2})^2+3\frac{1}{2}=\frac{21}{16}\end{displaymath}$

Solução do problema 3

$\begin{displaymath}d((1,4),(\frac{y^2}{2},y)^2=(1-\frac{y^2}{2})^2+(4-y)^2.\end{displaymath}$

Derivando:

$\begin{displaymath}d'(y)=-2(y-\frac{y^3}{2}+4-y)=y^3-8=0\end{displaymath}$

y=2

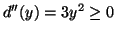
Mas $d''(y)=3y^2\geq 0$ e portanto este ponto é um mínimo. O ponto mais próximo é :

(2,2).

Solução do problema 4

Seja f(x)=x^2/3(6-x)^1/3Calculando as derivadas :

$\begin{displaymath}f'(x)=\frac{2}{3} x^{-1/3}(6-x)^{2/3}+\frac{1}{3}x^{2/3}(6-x)^{-2/3}(-1)= \end{displaymath}$

$\begin{displaymath}\frac{1}{3}(2(6-x)-x)=\frac{4-x}{x^{1/3}(6-x)^{2/3}}\end{displaymath}$

Calculando f''(x) obtemos:

$\begin{displaymath}f''(x)=\frac{-8}{x^{4/3}(6-x)^{5/3}}\end{displaymath}$

Observe que f'(x)=0 somente quando x=4 e que f' não está definida em x=0 e x=6. A seguinte análise de sinal mostra os intervalos de crescimento e decrescimento de f.

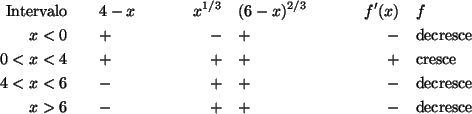
$\begin{align*}\text{Intervalo} \quad & \quad 4-x & \quad x^{1/3} & \quad (6-x)^{... ...quad & \quad - & \quad + & \quad + & \quad - & \quad\text{decresce} \end{align*}$
Como f' muda de sinal em 0 f(0)=0 é um mínimo local. Já em

$\begin{displaymath}x=4\quad f(4)=2^{5/3}\end{displaymath}$

é máximo. A ánalise de f'' mostra que f''(x)<0 para x<0 e para 0<x<6 e neste intervalo a função é côncava para baixo. Por outro lado f''(x)>0 para x>6 e no intervalo x>6 a função é côncava para cima.

b) f(x)=x⁴-4x³

Calculando f' e f'' temos:

$\begin{displaymath}f'(x)=4x^3-12x^2=4x^2(x-3)\qquad f''(x)=12x^3-24x=12x(x-2)\end{displaymath}$

Segue que x=0 e x=3 são pontos críticos. É fácil ver que f'(x)<0 para x<3 e que f'(x)>0 para x>3. A análise de f''(x) indica que f''(x)<0 para 0<x<2 e neste intervalo ela é côncava para baixo. No conjunto complementar ela será côncava para cima. O gráfico de f é como na figura abaixo:

**Figura 2:** Gráfico II
$\includegraphics[width=0.50\textwidth]{exer4.eps}$

Solução do problema 5

f(x)=x⁴-5x³+4x²-x+13

Começamos com x₀=2 já que f(2)=3 e f(3)=-8 havendo pois uma raiz entre 2 e 3.

f'(x)=4x³-15x²+8x-1

$\begin{displaymath}x_{n+1}=x_n-\frac{f(x_n}{f'(x_n)}\end{displaymath}$

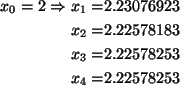
$\begin{align*}x_0=2\Rightarrow x_1=&2.23076923\\ x_2=& 2.22578183\\ x_3=& 2.22578253\\ x_4=&2.22578253 \end{align*}$

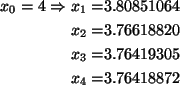
$\begin{align*}x_0=4\Rightarrow x_1=&3.80851064\\ x_2=& 3.76618820\\ x_3=& 3.76419305\\ x_4=&3.76418872 \end{align*}$

Solução do problema 6

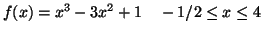
a) $f(x)=x^3-3x^2+1\quad -1/2\leq x\leq 4$

$\begin{displaymath}f'(x)=3x^2-6x=0\quad x=0\;\;x=2\end{displaymath}$

$\begin{displaymath}f(-\frac{1}{2})=\frac{1}{8}\quad f(0)=-3\end{displaymath}$

$\begin{displaymath}f(2)=-3\quad f(4)=17\end{displaymath}$

Segue que o máximo absoluto é f(4)=17 e o mínimo absoluto é f(2)=-3.

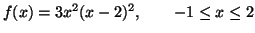
b) $f(x)=3x^2(x-2)^2,\qquad -1\leq x\leq 2$

f'(x)=6x(x-2)²+6x²(x-2)=12x((x-2)(x-1)=0

Os pontos críticos são: x=0, x=2 e x=1. e os valores de f nestes pontos são:

$\begin{displaymath}F(-1)=27,\;f(0)=0,\;f(1)=3,\;f(2)=0\end{displaymath}$

Máximo absoluto : M=27, Mínimo absoluto: m=0

Solução do problema 7

Seja x a distância entre o ponto mais próximo da lâmpada ao caminho e a posição do homem.

**Figura 3:** Lâmpada
$\includegraphics[width=0.50\textwidth]{exer7.eps}$

$\begin{displaymath}\frac{x}{20}=\tan \theta\Rightarrow x=20\tan \theta \end{displaymath}$

$\begin{displaymath}\frac{dx}{dt}=20\sec ^2 \theta \frac{d\theta}{dt}\end{displaymath}$

Logo,

$\begin{displaymath}\frac{d\theta}{dt}=\frac{1}{20}\cos^2\theta \frac{dx}{dt}=\frac{1}{5}\cos^2\theta\end{displaymath}$

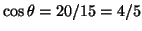
Quando x=15 usando triângulos temos que $\cos \theta=20/15=4/5$ e portanto:

$\begin{displaymath}\frac{d\theta}{dt}=\frac{1}{5}\left(\frac{4}{5}\right)^2=0.128\end{displaymath}$

que é a velocidade de rotação da lâmpada.

Solução do problema 8

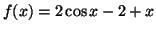Seja $f(x)=2\cos x-2+x$ .

$\begin{displaymath}f'(x)=1-2{\text {\ sen }}x\end{displaymath}$

$\begin{displaymath}x_{n+1}=x_n-\frac{f(x_n}{f'(x_n)}\end{displaymath}$

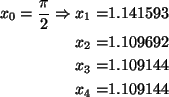
$\begin{align*}x_0=\frac{\pi}{2}\Rightarrow x_1=&1.141593\\ x_2=& 1.109692\\ x_3=& 1.109144\\ x_4=&1.109144 \end{align*}$

Solução do problema 9 Cálculo dos limites:

1.

$\begin{displaymath}\lim\limits_{x\to -3}\frac{x^4-81}{x-3}=\left(\frac{0}{0}\right)= \lim\limits_{x\to -3}\frac{4x^3}{1}=-108\end{displaymath}$

2.

$\begin{displaymath}\lim\limits_{x\to 0}\frac{{\text {\ sen }}x -x}{\tan x-x}=\le... ...im\limits_{x\to 0}\frac{-{\text {\ sen }}x }{2\sec ^2 x\tan x}=\end{displaymath}$

$\begin{displaymath}\lim\limits_{x\to 0}\frac{-\cos x}{2\sec ^4 x+4\tan ^2 x\sec^2 x}=-\frac{1}{2}\end{displaymath}$

3.

$\begin{displaymath}\lim\limits_{x\to 0}\left[\frac{1}{{\text {\ sen }}x}-\frac{1... ...{x\to 0}\frac{2x-\cos x}{2x{\text {\ sen }}x+x^2\cos x}=-\infty\end{displaymath}$

4.

$\begin{displaymath}\lim\limits_{x\to \infty}\frac{\sqrt{x^2-25}}{x^3+2}= \left(\... ...ght)= \lim\limits_{x\to \infty}\frac{x}{(x^2-25)^{1/2}(3x^2)}=0\end{displaymath}$

5.

$\begin{displaymath}\lim\limits_{x\to 0} x\ln(\tan x))=\lim\limits_{x\to \infty}\... ...\ln (\tan x)}{\frac{1}{x}}=\left(\frac{-\infty}{\infty}\right)=\end{displaymath}$

$\begin{displaymath}\lim\limits_{x\to \infty}-\frac{\sec^2 x}{x^{-2}\tan x}= \lim... ... {\ sen }}2x}= \lim\limits_{x\to \infty}-\frac{ 2x}{\cos 2x}=0 \end{displaymath}$

Lista XI Aplicações da Derivada Soluções

Lista XI
Aplicações da Derivada
Soluções