Soluções Lista V

Soluções:

Solução do Problema 1  

O volume de água na piscina em função de h, a altura quando h está próximo de 5 é

$$V(h)=h\cdot l\cdot \frac{1}{2}(12+12+h+\frac{16h}{6})$$

Como l=20 ft simplificando obtemos

$$V(h)=20\cdot h\cdot \frac{1}{2}\left(\frac{144+22h}{6}\right)$$

isto é

$$V(h)=\frac{720h+122h^2}{3}$$

Derivando implicitamente obtemos:

$$\frac{dV}{dt}=\left(24+\frac{244h}{3}\right)\frac{dh}{dt}$$

Como $\frac{dV}{dt}=0.8 ft/min$ temos

$$\frac{dh}{dt}=\frac{3\frac{dV}{dt}}{720+244h}$$

isto é

$$\frac{dh}{dt}=\frac{3\frac{dV}{dt}}{720+244h}=\frac{2.4}{1940}=0.012 ft/min$$

 

Figure 1: Piscina

Solução do Problema 2  

A variação do volume de água é dada pela fórmula

$$\frac{dV}{dt}={\text{entra}}-{\text{sai}}$$

$$\frac{dV}{dt}=tx_e(t)-10000$$

Por outro lado como o volume de um cone é $V=\frac{1}{3}\pi r^2 h$ e da figura sabemos que $\frac{4}{r}=\frac{6}{h}$ temos que $r=\frac{2}{3}h$ e portanto

$$V=\frac{1}{3}\pi \left(\frac{2h}{3}\right)^2 h=\frac{4\pi h^3}{27}$$

que derivando implicitamente obtemos

$$\frac{dV}{dt}=\frac{4\pi h^2 \frac{dh}{dt}}{9}=tx_e(t)-10000$$

logo a taxa de entrada no momento em que a altura era 200cm era

$$tx_e=\left(\frac{4\pi (200)^2 20}{9}+10000\right)cm^3/min$$

Solução do Problema 3  

Usamos a figura e a lei dos cossenos para expressar a distância entre os dois e obter:

$$d^2=A^2+B^2-A B\cos \theta= 10^4+4\cdot 10^4-2\cdot 10^4\cos \theta=10^4(5-2\cos \theta)$$

Derivando implicitamente obtemos

$$2dd'=10^4(2{\text {\ sen }}\theta) \frac{d\theta}{dt}$$

e então

$$d'=\frac{10^4 {\text {\ sen }}\theta}{d}\frac{d\theta}{dt}.$$

Mas como $s=r\theta$ temos $\frac{ds}{dt}=r\frac{d\theta}{dt}$ e como $\frac{ds}{dt}=7$ m/s temos que $\frac{d\theta}{dt}=\frac{1}{r}\frac{ds}{dt}= 7\frac{1}{r}=\frac{7}{100}$. Finalmente sabendo que a distância entre eles era 200 m podemos determinar o ângulo $\theta$ a saber:

$$220^2=100^2+200^2-2\cdot 10^4\cos \theta$$

$$\cos \theta=\frac{1}{2}$$

implicando que $\theta=\frac{\pi}{2}$. Portanto

$$d'=\frac{10^4 {\text {\ sen }}\frac{\pi}{3}}{200}\cdot 7\cdot... ...{2}{\text {\ sen }}\frac{\pi}{3}=\frac{7}{2}\frac{\sqrt{3}}{2}.$$

Solução do Problema 4  

Como f(x)=1-x² e f'(x)=-2x temos que uma das tangentes, a que passa no ponto Q=(x,1-x²) tem equação

w-1+x²=-2x(v-x).

Portanto os pontos A e C são obtidos fazendo v=0 e então w=1-x²+2x²=1+x², isto é A=(0,1+x²) e fazendo w=0 e neste caso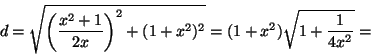

$$\frac{x^2-1}{-2x}=u-x\Rightarrow u=\frac{x^2+1}{2x}$$

isto é $B=(\frac{x^2+1}{2x},0)$. A distância entre os dois é portanto:

$$d=\sqrt{\left( \frac{x^2+1}{2x}\right)^2+(1+x^2)^2}=(1+x^2)\sqrt{1+\frac{1}{4x^2}}=$$

$$\frac{1+x^2}{2x}\sqrt{1+4x^2}$$

e como o triângulo deve ser equilátero devemos ter:

$$d=\frac{1+x^2}{2x}\sqrt{1+4x^2}=\frac{1+x^2}{x}$$

que resolvendo obtemos $\sqrt{1+4x^2}=2$ isto é 1+4x²=4 e portanto

$$x=\frac{\sqrt{3}}{2}.$$

Segue que os pontos são: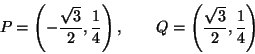

$$P=\left(-\frac{\sqrt{3}}{2},\frac{1}{4}\right),\qquad Q=\left(\frac{\sqrt{3}}{2},\frac{1}{4}\right)$$

Solução do Problema 5  

Sejam y_h(t) a posição do homem sobre o eixo-y no instante t e (500,y_m(t)) a da mulher que se desloca sobre a vertical x=500. Como as velocidades são respectivamente v_h=4 e v_m=5 tem-se que

$$y_h(t)=4t\qquad y_m(t)=-5(t-300).$$

Da figura ve-se que

d²=[y_h(t)-y_m(t)]²+500²

que derivando implicitamente temos

dd'=[y_h-y_m](y_h'-y_m')

Logo:

$$d'=\frac{[y_h-y_m](y_h'-y_m')}{\sqrt{[y_h(t)-y_m(t)]^2+500^2}}= \frac{(y_h'-y_m')}{\sqrt{1+\frac{500^2}{[y_h(t)-y_m(t)]^2}}}$$

No instante t=15 como $y_h=4\cdot 15\cdot 60=60^2$ e $y_m=-5(15-5)60=-50\cdot 60$ tem-se que:

$$d'=\frac{9}{\sqrt{1+\frac{500^2}{[60^2+50.60]^2}}}$$

Solução do Problema 6  

Da figura temos: R²=r²+h² e portanto $h=\sqrt{R^2-r^2}$. Como o volume de um cilindro é dado por $V=\pi r^2 h$ temos:

$$V=\pi r^2 \sqrt{R^2-r^2}$$

Derivando obtemos

$$V'(r)= 2\pi r \sqrt{R^2-r^2}+ \pi r^2 \frac{-2r}{2\sqrt{R^2-r^2}}=$$

$$\pi r\left[ 2\sqrt{R^2-r^2}-\frac{r^2}{\sqrt{R^2-r^2}}\right]=$$

$$\pi r \left[ \frac{2(R^2-r^2)-r^2}{\sqrt{R^2-r^2}}\right]=0$$

isto é

2R²-3r²=0

e portanto $r^2=\frac{2}{3}R^2$

$$r=R\sqrt{\frac{2}{3}}.$$

Portanto o volume máximo é

$$V_{{\text{m\'ax}}}=\pi \frac{2}{3}R^2 \frac{1}{\sqrt{3}}R= \frac{2\pi}{3\sqrt{3}}R^3$$

Solução do Problema 7  

Da figura, se denotamos y(t) e x(t) as posições dos barcos cujas velocidades são respectivamente 20km/h e 15 km/h temos que

$$y(t)=20(t-2)\qquad x(t)=15t+x_0$$

como x(3)=0 temos x(3)=45-x₀=0 e portanto x₀=-45 o que acarreta x(t)=15t-45. Logo a distância entre eles será dada por:

$$d=\sqrt{y(t)^2+x(t)^2}$$

que derivando obtemos:

$$d'=\frac{2y(t)y'(t)+2x(t)x'(t)}{2\sqrt{y(t)^2+x(t)^2}}= \frac{y(t)y'(t)+x(t)x'(t)}{\sqrt{y(t)^2+x(t)^2}}$$

e igualando a zero temos:

$$d'=\frac{(20(t-2))20+(15t-45)15}{\sqrt{(20(t-2))^2+(15t-45)^2}}=0$$

isto é 400(t-2)+225(t-3)=0 625t=800+675cuja solução é:

$$t=\frac{1475}{625}=2.36$$

Solução do Problema 8  

Para responder a) derivamos S para obter:

$$\frac{dS}{dt}=-\frac{3}{2}s^2(-({\text {\ cossec }}^2 \theta)... ...rt{3}}{2} (-{\text {\ cossec }}\theta {\text {\ cotg }}\theta).$$

Para responder b) igualamos o resultado obtido a zero

$$\frac{3}{2}s^2({\text {\ cossec }}^2 \theta)-3s^2\frac{\sqrt{... ...[\frac{1}{2}-\frac{\sqrt{3}}{2}{\text {\ cotg }}\theta\right]=0$$

donde temos

$$\frac{1}{2}-\frac{\sqrt{3}}{2}{\text {\ cotg }}\theta=0$$

isto é ${\text {\ cotg }}\theta =\frac{1}{\sqrt{3}}$ a saber as abelhas preferem o ângulo

$$\theta_0=\text{arc\;{\text {\ tg }}}\sqrt{3}.$$

Da trigonometria sabemos que

$${\text {\ cossec }}\theta =\frac{\sqrt{1+{\text {\ tg }}^2\theta}}{{\text {\ tg }}\theta}$$

e portanto

$$S=6sh-\frac{3}{2}s^2 \frac{1}{\sqrt{3}}+ +3s^2\frac{\sqrt{3}}{2} \frac{2}{\sqrt{3}}$$

$$S=6sh +3s^2\left(1-\frac{1}{2\sqrt{3}}\right).$$

Solução do Problema 9  

Como y=x² e y'=2x a reta tangente à parábola no ponto (x,x²)será:

w-x²=2x(v-x).

Como esta reta deverá conter o ponto onde está a estátua que é (100,50) devemos ter:

50-x²=2x(100-x)

isto é

x²-200x+50=0

cuja solução que nos interessa é

$$x_1=\frac{200-\sqrt{39800}}{2}=0.25$$

e portanto o ponto sobre a estrada no qual os faróis iluminarão diretamente a estátua é

(0.25, 0.25²).

Solução do Problema 10  

Vamos assumir que o quadrado tem lado x e que o círculo tem raio r. Então sabemos que $4x+2\pi r=16$ e portanto $r=(16-4x)/2\pi=(8-2x)\pi$. A área total é

$$A(x)=x^2+\pi r^2=x^2+\pi\left(\frac{8-2x}{\pi}\right)^2=\frac{1}{\pi}\left((4+\pi)x^2-32x+64\right).$$

Calculando a derivada obtemos:

$$A'(x)=\frac{2}{\pi}((4+\pi)x-16),$$

e portanto o único ponto crítico ocorre em $x=16/(4+\pi)$. Como estamos tratando com uma função quadrática com coeficiente do termo quadrático positivo sabemos que este é um ponto de mínimo. Portanto o corte deverá ser feito a 4x unidades da extremidade esquerda isto é a distância de

$$\frac{64}{(4+\pi)}$$

desta extremidade.

Solução do Problema 11  

Se o cilindro (e portanto a abóboda) tem raio r e altura h, então o volume do observatório será

$$V=\pi r^2 h+\frac{2}{3}\pi r^3.$$

Logo

$$h=\frac{V}{\pi r^2}-\frac{2r}{3}.$$

A área da superfície cilindrica é $2\pi rh$ e a da abóboda $2\pi r^2$. Portanto para minimizarmos o custo da obra devemos minimizar a função:

$$C(r)=2\pi rh+2(2\pi r^2)=$$

$$2\pi \left(\frac{V}{\pi r^2}-\frac{2r}{3}\right)+ 4\pi r^2= \frac{2V}{r }-\frac{8\pi r^2}{3}.$$

Derivando e derivando mais uma vez obtemos:

$$C'(r)=-\frac{2V}{r^2 }+\frac{16\pi r}{3}=0\qquad \quad C''(r)=\frac{4V}{r^3 }+\frac{16\pi}{3}.$$

Segue que o ponto crítico de C ocorre quando $r^3=\frac{3V}{8\pi}$ e que neste ponto a derivada segunda é negativa sendo portanto um mínimo. Logo a configuração mais econômica se dá quando

$$r=\sqrt[3]{\frac{3V}{8\pi}}.$$

BACK TO CALCULUS A PAGE

BACK TO MATHBIO PAGE