

Next: Integração
Up: Propriedades da medida de
Previous: Distorção da medida de
Estando provadas as propriedades mais importantes da medida de Lebesgue
algumas questões pertinentes se colocam. A mais importante delas é o
problema da extensão da medida de Lebesgue. Mais precisamente:
Problema I. Existem 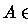 -álgebra
-álgebra
 e
e
![$\mu:\ensuremath\boldsymbol{ \mathscr{A} } \rightarrow [0,+\ensuremath{\infty } ]$](img223.gif) uma medida tal que
uma medida tal que
e
A resposta a este problema é não como mostra o teorema:
Teorema 3.3.1
Se
é uma
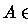
-álgebra de subconjuntos de
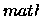
que contém os cubos e
tal que
então
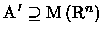
.
Problema II Existe uma medida
sendo
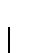 a
a 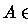 -álgebra de
-álgebra de
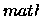 , contendo propriamente
, contendo propriamente
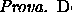 e tal que
e tal que
Observe que pelo teorema anterior 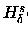 não pode ser uma restrição da medida exterior de Lebesgue. A resposta neste caso é afirmativa
e segue do resultado:
não pode ser uma restrição da medida exterior de Lebesgue. A resposta neste caso é afirmativa
e segue do resultado:
Teorema 3.3.2 (Kakutani-Oxtoby)
Exite uma
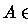
-álgebra

e uma medida
que estende a medida de Lebesgue. Além disto,
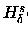
e
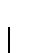
satisfazem:
se
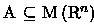
é uma bijeção tal que
- 1.
-

- 2.
-

então,
T satisfaz as mesmas propriedades substituindo-se
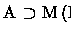
por
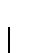
.
Em particular a extensão de Kakutani-Oxtoby é invariante por isometrias. Por
outro lado a medida de Lebesgue não admite extensões próprias se exigimos
que a extensão seja uma medida regular.
Definição 3.3.1
Uma medida
![$\mu:\ensuremath\boldsymbol{ \mathscr{A} } \rightarrow [0,+\ensuremath{\infty } ]$](img223.gif)
onde
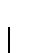
é uma
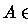
-álgebra de um espaço
topológico que contém os boreleanos é
regular se

Teorema 3.3.3
Se
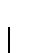
é uma
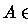
-álgebra de
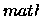
contendo os cubos de
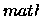
e
![$\mu\colon\ensuremath\boldsymbol{ \mathscr{A} } \rightarrow [0,+\ensuremath{\infty } ]$](img238.gif)
é uma medida regular tal que
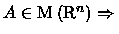
para
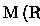
cubo então


Next: Integração
Up: Propriedades da medida de
Previous: Distorção da medida de
Aldrovando Azeredo Araujo
1998-03-19
 e
e
![]() -álgebra
-álgebra
 e
e
![]() uma medida tal que
uma medida tal que
![]() não pode ser uma restrição da medida exterior de Lebesgue. A resposta neste caso é afirmativa
e segue do resultado:
não pode ser uma restrição da medida exterior de Lebesgue. A resposta neste caso é afirmativa
e segue do resultado: e uma medida
e uma medida
