Se você chegou nesta página deveria estar com o Maxima instalado em seu PC (senão instale !!!). Se você ainda não está familiarizado com um  CAS (Computer Algebra System: Sistema de Computação Algébrica)  Maxima oferece uma excelente oportunidade para resolver essa carência.
Quando comece a transitar por este Tutorial  você começará a perceber  que está  lidando com uma ferramenta matemática que será de grande ajuda em sua carreira como estudante.  Maxima é muito amigável e um passeio por este tutorial mínimo pode ajudar a eliminar aquelas duvidas sobre se o investimento em aprender a usar um software matemático terá um bom retorno, são apenas 10 minutos que  o colocarão no caminho certo. 
Este Tutorial oferece uma abordagem prática e rápida onde é mostrado como resolver computacionalmente alguns problemas  mais comuns encontrados em Cálculo, Álgebra Linear, etc. Claro que é apenas a ponta do iceberg. Uma vez que você tenha transitado por este tutorial o próximo passo será visitar o site oficial de Maxima.

Usando Maxima como uma calculadora

Você pode usar Maxima como uma calculadora cuja precisão dependerá  do hardware instalado em  seu  PC. O promt do Maxima aguardará que você ingresse um ou mais comandos e expressões separadas por ponto e vírgula (;), exatamente como você faria em qualquer linguagem de programação.

(%i1) 9+7;

(%o1) 16
(%i2) -17*19;
(%o2) -323
(%i3) 10/2;
(%o3) 5

Maxima permite fazer referência ao último resultado através do caractere % , e também a qualquer entrada ou saída através de seu respectivo promt %i (input: entrada) ou %o (output: saída). Por exemplo:

(%i4) % - 10;

(%o4) -5
(%i5) %o1 * 3;
(%o5) 48

(Obs.: Com o intuito de que os comandos e expressões nos próximos exemplos  fiquem visualmente mais simples e claros,  omitiremos por agora a numeração de entradas e saídas retornadas pelo Maxima indicando a saída com o sinal de implicação => .)
Quando o  numerador e  denominador são inteiros, é devolvida uma expressão como uma fração reduzida o um inteiro. Esse resultados podem ser  re-calculados em ponto flutuante usando o comando  float  (ou bfloat para  números grande em ponto flutuante):

8/2;

=> 4

8/2.0;

=> 4.0

2/6;

=> \displaystyle \frac{1}{3}

float(1/3);

=> 0.33333333333333

1/3.0;

=> 0.33333333333333

26/4;

=> \displaystyle \frac{13}{2}

float(26/4);

=> 6.5

Como foi dito, números grandes não são um problema:

13^26;

=> 91733330193268616658399616009

13.0^26

=> \displaystyle 9.1733330193268623\text{ }10^_{+28}

30!;

=> 265252859812191058636308480000000

float((7/3)^35);

=> \displaystyle 7.5715969098311943\text{ }10^_{+12}

Constantes e funções mais usuais

Aqui temos uma lista das constantes em Maxima, :

§  %e - Número de Euler

§  %pi - \displaystyle \pi

§  %phi - a seção dourada (\displaystyle \frac{1+\sqrt{5}}{2})

§  %i - a unidade imaginária (\displaystyle \sqrt{-1})

§  inf - infinito positivo (\infty)

§  minf - infinito negativo  (-\infty)

§  infinity - infinito complexo

Algumas das funções mais usadas:

sin(%pi/2) + cos(%pi/3);

=> \displaystyle \frac{3}{2}

tan(%pi/3) * cot(%pi/3);

=> 1

float(sec(%pi/3) + csc(%pi/3));

=> 3.154700538379252

sqrt(81);

=> 9

log(%e);

=> 1

Definindo funções e variáveis

As variáveis podem ser designadas usando dois pontos ‘:’ e as funções ‘:=’. A seguinte sequência mostra como usá-las:

a:7; b:8;

=> 7

=> 8

sqrt(a^2+b^2);

=> \sqrt{113}

f(x):= x^2 -x + 1;

=> x^2 -x + 1

f(3);

=> 7

f(a);

=> 43

f(b);

=> 57

Observamos que Maxima calcula por default o logaritmo natural entanto que  a função log 10 não está definida e deve ser calculada como se mostra a seguir:

log10(x):= log(x)/log(10);

=> \displaystyle log10(x):=\frac{log(x)}{log(10)};

log10(10)

=> 1

Cálculos Simbólicos

O comando factor possibilita a fatoração de um número:

factor(30!);

=> \displaystyle 2^{26}\,3^{14}\,5^7\,7^4\,11^2\,13^2\,17\,19\,23\,29

Podemos fatorar um polinômio:

factor(x^2 + x -6);

=> (x-2)(x+3)

Fazer a expansão:

expand((x+3)^4);

=> \displaystyle x^4+12\,x^3+54\,x^2+108\,x+81

Simplificar expressões racionais:

ratsimp((x^2-1)/(x+1));

=> x-1

Simplificar expressões trigonométricas:

trigsimp(2*cos(x)^2 + sin(x)^2);

=> \displaystyle \cos ^2x+1

Expandir expressões trigonométricas:

trigexpand(sin(2*x)+cos(2*x));

=> \displaystyle -\sin ^2x+2\,\cos x\,\sin x+\cos ^2x

Para obter a  representação  em  LaTeX  de uma expressão dada, usamos o comando  tex :

tex(%);

=> $$-\sin ^2x+2\,\cos x\,\sin x+\cos ^2x$$

Resolvendo Equações e Sistemas

Com o comando solve podemos resolver equações  e sistemas de equações :

solve(x^2-4,x);

=> \displaystyle \left[ x=-2 , x=2 \right]

%[2]

=> x=2

solve(x^3=1,x);

=> \displaystyle \left[ x={{\sqrt{3}\,i-1}\over{2}} , x=-{{\sqrt{3}\,i+1}\over{2}}  , x=1 \right]

trigsimp(solve([cos(x)^2-x=2-sin(x)^2], [x]));

=> \displaystyle \left[ x=-1 \right]

solve([x - 2*y = 14,  x + 3*y = 9],[x,y]);

=> \left[ \left[ x=12 , y=-1 \right]  \right]

Gráficos em 2D e 3D

Maxima faz gráficos bi e tri-dimensionais, e também múltiplos gráficos em uma mesma folha. Os comandos plot2d e  plot3d são usados nos exemplos abaixo. O segundo  e no caso de  plot3d, o terceiro parâmetro, define o intervalo de variação de  x e y respectivamente e define qual é a parte do gráfico que será mostrada.

plot2d(x^2-x+3,[x,-10,10]);

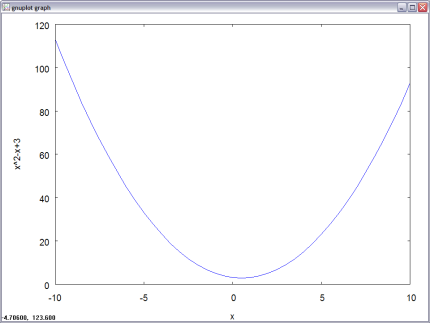
2dplot.png

plot2d([x^2, x^3, x^4 -x +1] ,[x,-10,10]);

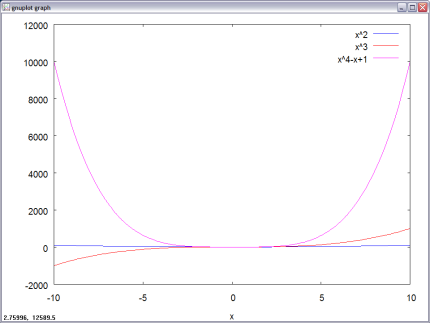
many_2dplot.png

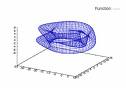
f(x,y):= sin(x) + cos(y);

plot3d(f(x,y), [x,-5,5], [y,-5,5]);

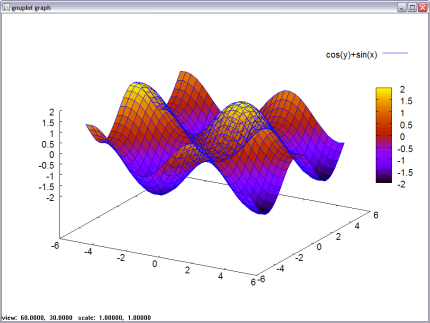
3dplot.png

Limites

limit((1+1/x)^x,x,inf);

=> %e

limit(sin(x)/x,x,0);

=> 1

limit(2*(x^2-4)/(x-2),x,2);

=> 8

limit(log(x),x,0,plus);

=> -\infty

limit(sqrt(-x)/x,x,0,minus);

=> -\infty

Diferenciação

diff(sin(x), x);

=> \displaystyle cos(x)

diff(x^x, x);

=> \displaystyle x^{x}\,\left(\log x+1\right)

É possível calcular derivadas de maior ordem acrescentando o número  correspondente como um argumento do comando diff :

diff(tan(x), x, 4);

=> \displaystyle 8\,\sec ^2x\,\tan ^3x+16\,\sec ^4x\,\tan x

Integração

Maxima oferece realizar várias formas de integração. Para encontrar a primitiva de uma função use integrate:

integrate(1/x, x);

=> \displaystyle log(x)

Para calcular uma integral definida, devemos especificar os limites de integração como os últimos parâmetros:

integrate(x+2/(x -3), x, 0,1);

=> \displaystyle -2\,\log 3+2\,\log 2+{{1}\over{2}}

integrate(%e^(-x^2),x,minf,inf);

=> \sqrt{\% pi}

Também a integral definida pode ser obtida aproximadamente usando um método numérico(por ex.  romberg):

romberg(cos(sin(x+1)), x, 0, 1);

=> 0.57591750059682

Somas e Produtos

sum e product são duas funções para realizar  somatórios e produtórias. A opção simpsum simplifica a soma quando for possível.

sum(k, k, 1, n);

=> \displaystyle \sum_{k=1}^{n}{k}

sum(k, k, 1, n), simpsum;

=> \displaystyle {{n^2+n}\over{2}}

sum(1/k^4, k, 1, inf), simpsum;

=> \displaystyle {{\%pi^{4}}\over{90}}

fact(n):=product(k, k, 1, n);

=> fact(n):=product(k,k,1,n)

fact(10);

=>  3628800

Expansão em Séries

 A representação de uma função em série de potências pode ser obtida usando a expansão de Taylor  (o último parâmetro define a ordem da série), os comando usados são taylor ou  powerseries:

niceindices(powerseries(%e^x, x, 0));

=> \displaystyle \sum_{i=0}^{\infty }{{{x^{i}}\over{i!}}}

taylor(%e^x, x, 0, 5);

=> \displaystyle 1+x+{{x^2}\over{2}}+{{x^3}\over{6}}+{{x^4}\over{24}}+{{x^5}\over{120 }}+\cdots

O comando trunc combinado com  plot2d  é usado quando a expansão precisamos graficar a série:

plot2d([trunc(%), %e^x], [x,-5,5]);

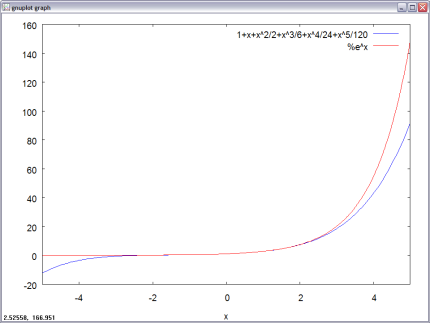
taylor.png

O material desta página pretende apenas mostrar as facilidades que oferece o uso de um software como Maxima. Os sistemas de computação algébrica são ferramentas poderosas para resolver problemas  e testar resultados e o tempo que você terá investido terá um retorno muito maior que o esperado.