1.1 Introdução

A computação algébrica é um novo meio de aprendizado que une a informática ao ensino da Matemática. Este novo método de ensino das ciências exatas e de Matemática em particular, vem sendo adotado em diversas universidades e ocupa posição de destaque no mundo educacional de países desenvolvidos. As universidades estrangeiras ministram cursos regulares de computação algébrica aos alunos destinados à área de ciências exatas, o que é uma medida clara da importância que o meio científico e tecnológico vem adquirindo neste ramo.

A capacidade de armazenamento de informações, a velocidade de operação e a precisão faz do uso do computador uma ferramenta indispensável em todas as nossa atividades acadêmicas, profissionais e domésticas. Porém, ensinar o aluno somente a operar no computador não garante a melhoria da qualidade do ensino. É de suma importância que nossos es-tudantes estejam ao menos familiarizados com essa tecnologia, pois, afinal, deles depende o futuro de nossa sociedade. Uma das principais razões do uso do computador na educação é desenvolver o raciocínio e possibilitar situações de resolução de problemas, a fim de desenvolver o pensamento do aluno. O computador não deve ser inserido na educação como uma máquina de ensinar ou uma informatização instrucionista. Deve ser usado como uma informatização construcionista, que permita a reflexão e a construção de idéias, a partir da relação professor, computador e aluno. Deve-mos levar em conta que o computador não é o principal referencial do processo de ensino-aprendizagem, mas serve apenas como uma ferramenta auxiliar.

No mercado de informática existem vários softwares (pacotes computacionais) que oferecem condições de cálculos numéricos, manipulações algébricas e simbólicas. Alguns destes softwares funcionam no sistema operacional DOS e/ou são feitos para Windows. Os softwares Mathematica, Maple, Derive, etc., são sistemas de computação algébrica muito eficientes como apoio ao ensino de Cálculo, e vêm sendo utilizados por exemplo, nas fases iniciais dos cursos de Engenharia, Computação, Física e Matemática, em universidades estrangeiras, proporcionando aos alunos maior interesse e compreensão. Os dois primeiros pacotes são feitos para Windows, e o Derive funciona no sistema operacional DOS.

No que se refere ao processo ensino-aprendizagem esses pacotes computacionais exercem grande influência no desenvolvimento intelectual dos alunos. Este recurso didático apresenta a facilidade de construção de gráficos de funções e resoluções dos problemas, bem como no aprendizado da montagem das equações a resolver, e da previsão de seu comportamento, e soluções. Os softwares possibilitam, além de uma melhor visualização gráfica, a apresentação de tópicos avançados e de suas muitas aplicações práticas. Esta grande ferramenta matemática permite ao estudante uma compreensão mais nítida dos processos e potencialidades do Cálculo Diferencial e Integral, auxiliando-o em seus estudos.

Os potentes pacotes computacionais Mathematica e Maple não são restritivos ao Cálculo Diferencial e Integral, pois também se aplicam em diversas áreas da Matemática, Física, Engenharia, etc.. Outros tópicos básicos relacionados com Matemática que podem ser abordados facilmente são: Álgebra Linear, Equações Diferenciais, Séries Infinitas, etc.

Neste capítulo apresentamos os conceitos básicos de matemática utilizando o software Mathematica.

1.2 Utilização do software Mathematica

Este trabalho teve como base a utilização do software Mathematica versão 2 para Windows. Sendo assim, serão aqui apresentadas noções básicas somente para sua utilização nesta versão. Será considerado que o usuário já tenha algum conhecimento de utilização de softwares para Windows. Caso não o possua, é aconselhável que o adquira antes de começar a utilizar o Mathematica, pois não serão abordadas as características comuns a todos os softwares para Windows.

Uma vez que o programa esteja iniciado, tem-se então a tela inicial do programa, que consiste de um menu com as opções disponíveis e uma área de trabalho. A grande maioria dos comandos do Mathematica utilizados nesta apostila são comandos internos, ou disponíveis em pacotes, que são digitados e executados na área de trabalho.

Para executar um comando basta digitá-lo, e então pressionar a combinação das teclas SHIFT + ENTER ou tecla 5 do lado direito com o Num Lock desativado ou clique acima do ícone do poliedro dado na tela do Mathematica. Neste momento, o texto digitado é considerado como uma entrada, e será então dada uma saída, que aparecerá imediatamente abaixo da entrada. Caso ocorra algum erro de execução, ou de sintaxe, uma mensagem apropriada será dada como saída. Deve-se tomar muito cuidado na hora de digitar um comando, pois são consideradas as diferenças entre letras maiúsculas e minúsculas, sendo que, muitas vezes, este é o motivo de vários erros na hora de sua execução. No capítulo a seguir, veremos os conceitos básicos de Matemática utilizando o software Mathematica.

1.3 Operações básicas

O software Mathematica possui diversos recursos para realizar as operações básicas, funcionando em parte semelhante a uma calculadora. As operações que vamos trabalhar nesta primeira etapa referem-se às "operações básicas". São elas: "adição (+)", "subtração (- )", "divisão( / )", "multiplicação (*)", "potenciação (^)", etc. Também apresentamos utilização de "potenciação". Em cada caso para resolvê-la, digite o sinal desejado entre os números e pressione a combinação das teclas SHIFT + ENTER ou tecla 5 do lado direito com o Num Lock desativado ou clique acima do ícone do poliedro dado na tela do Mathematica no final da operação para ter a resposta desejada.

* Adição:  O sinal " +" significa adição; 3 + 7 é 3 mais 7.

* Subtração:  O sinal " - "  significa subtração; 8 - 7 é 8 menos 7.

* Divisão:  O sinal "/" significa divisão (ou fração); 5/17 é 5 dividido por 17.

* Multiplicação: O símbolo " * "  significa multiplicação; 34*89 é 34 vezes 89. Alternativamente, um espaço também pode ser usado para indicar multiplicação. Isto é, 22 35 é a mesma coisa que 22*35; 2 5 significa 2 vezes 5 e 5 8 9 significa 5 vezes 8 vezes 9. Veja a seguir alguns exemplos:

* Potenciação: O símbolo "^" significa potenciação; 4^3 é quatro elevado à terceira potência.

* Expressões com várias operações: Este caso inclui todas as operações dadas acima, apresentamos alguns exemplos a seguir:

a)  In[ ]:= 5^3 - 3.11 + 5/4 - 15*3.2
      Out[ ]= 75.14

b)  In[ ]:= 4^(1/2) + 3.27 - (14+3/2)/5
      Out[ ]= 2.17

Observações

·  Em símbolos computacionais o "ponto" substitui a "vírgula" na representação de números decimais, como na calculadora normal.

·  "In[ ]:=" é um comando embutido no Mathematica e significa entrada. "Out[ ]="  também é um comando embutido no Mathematica e significa saída, ou melhor, a resposta da operação ou da execução do comando.

·  A operação da multiplicação pode ser indicada pelo símbolo " * " ou por um espaço vazio.

·  Quando a multiplicação envolve números e variáveis, não é necessário dar espaço, isto é, 4x ou 4 x representa a mesma coisa.

·  Multiplicação separada com parênteses não necessita de espaço, isto é, (x- 2) (x- 5) ou (x- 2)(x- 5) é a mesma coisa.

·  A quantidade (- 1)^2/3 é diferente de (- 1)^(2/3), isto é, (- 1)^2/3 significa enquanto que a operação (-1)^(2/3) indica . Para evitar confusões é conveniente utilizar ((- 1)^2)/3 em vez de (- 1)^2/3.

·  A representação decimal tem preferência em relação à fração, se houver uma entrada em decimal. Ela dá resposta em decimal, mesmo que haja entradas fracionárias, independente de outras operações (veja exemplos de expressões com várias operações).

·  Se quisermos as respostas de uma expressão na forma de números decimais, devemos usar o comando "N[k]", onde k é um número, a função ou a expressão. Para especificar o número de dígitos, escrevemos "N[k,n]", onde n é um inteiro positivo. O comando "//N" também é usado para calcular valores decimais aproximados. Veja alguns exemplos a seguir:

a) In[ ]:= N[2/3]
     Out[ ]= 0.666667

b) In[ ]:= N[2/5,20]
     Out[ ]= 0.4

c) In[ ]:= N[22/15,10]
     Out[ ]= 1.466666667

d)  In[ ]:= N[Pi]
      Out[ ]= 3.14159

e) In[ ]:= N[Pi,12]
     Out[ ]= 3.14159265359

f) In[ ]:= 2^100
    Out[ ]= 1267650600228229401496703205376

g) In[ ]:= 2^100//N
    Out[ ]= 1.26765 10³⁰

1.4 Algumas representações importantes

( )       (Parênteses) são utilizados somente para indicar ordem entre operações: por exemplo, (x+3)/x é             entendido como . Não se deve utilizar colchetes ou chaves para indicar ordem entre             operações. Utilize somente parênteses.

[ ]        (Colchetes) são utilizados entre funções e comandos: por exemplo, Sin[x] representa o seno de x.              Sin(x) não é aceito.

{ }         (Chaves) indicam listas: por exemplo, {1,3,5,7} é uma lista de quatro números.

%       representa o resultado do último cálculo efetuado. Este símbolo pode ser usado várias vezes. Se            usarmos o símbolo " % ", a nova operação será realizada com o resultado do último cálculo             efetuado.

%%    representa o resultado do penúltimo cálculo efetuado, por exemplo:

a) In[ ]:= 3*7
       Out[ ]= 21

b)  In[ ]:= %^2
       Out[ ]= 441

c) In[ ]:= %%*2
     Out[ ]= 42

 %%%   representa o antepenúltimo resultado. Logo, o símbolo " % " pode ser usado sucessivamente, tantas vezes quantas              desejarmos.

 /.          significa substituir o valor da variável por um valor constante.

 !           significa fatorial: Assim 5! é fatorial de 5.

 =          representa atribuição: a=5 significa atribuir o valor 5 para a.

 :=         também representa atribuição para avaliar a expressão mais vezes, e em diferentes momentos.

 ==        significa o sinal de igualdade:

 <, <=, > e >=   significam, respectivamente: menor, menor ou igual, maior e maior ou igual.

 Observação

•  A diferença entre os dois símbolos de atribuição descritos acima, está no fato de que "=" é utilizado quando a expressão que está à sua direita é avaliada apenas uma vez, enquanto que ":=" é utilizado quando queremos avaliar a expressão mais vezes, e em diferentes momentos.

1.5 Ajuda

Quando necessitarmos de alguma ajuda a um comando específico, devemos digitar um ponto de interrogação no início do comando, e acionar SHIFT+ENTER ou tecla 5 do lado direito com Num Lock desativado ou clique com mouse em cima do ícone de poliedro aparecendo na tela de Mathematica. Então recebemos as instruções em relação àquele comando específico. Também podemos ter ajuda diretamente clicando com mouse na palavra "Help". .

Alguns exemplos de procurar ajuda em relação à existência dos comandos, o que é feito utilizando "?", "??" e "*", tais como: "?Plot", "??Plot", "?Plot*", "?*Plot", ?*Plot*", "?*3D*", "?Plot3D", etc.. Por exemplo,

In[ ]:= ?Plot

1.6 Conjuntos

O conceito primitivo de conjunto é assunto de grande importância em Matemática. Podemos representá-lo de diversas maneiras, entre elas por extensão, isto é, quando ocorre a listagem de seus elementos. Para tratar de conjuntos finitos, o software Mathematica, tem uma série de comandos: "Lista", "Max", "Min", "Length", "Intersection", "Union", "Complement", "Join" etc., cujas explicações veremos no final desta seção. A seguir daremos alguns exemplos de conjuntos onde utilizamos os comandos dados acima para calcular seus respectivos valores necessitados:

Exemplo 1.1

Seja U₁ = {3,4,5,9,7,12} um conjunto. Encontrar
i) elemento máximo de U₁;
ii) elemento mínimo de U₁;
iii) conjunto com quadrado dos elementos de U₁;
iv) conjunto com metade dos elementos de U₁;
v) número de elementos do conjunto U_1.

Resolução

Para resolver este exemplo inicialmente definimos o conjunto U₁ dando o seguinte comando:

In[ ]:= U1={3, 4, 5, 9, 7, 12}
Out[ ]= {3, 4, 5, 9, 7, 12}

 i) In[ ]:= Max[u1]
     Out[ ]= 12

ii) In[ ]:= Min[u1]
     Out[ ]= 3

iii) In[ ]:= U1^2
        Out[ ]= {9, 16, 25, 81, 49, 144}

iv) In[ ]:= U1/2
      Out[ ]= {, 2, , , , 6}

v) In[ ]:= Length[U1]
     Out[ ]= 6

 Assim, concluímos que

• elemento máximo de U₁ é 12;
• elemento mínimo de U₁ é 3;
• conjunto com quadrado dos elementos de U₁ é {9, 16, 25, 81, 49, 144};
• conjunto com metade dos elementos de U₁ é {, 2, , , , 6};
• número de elementos do conjunto U₁ são 6.

Exemplo 1.2

Sejam U₃ = { -1, 3, -8, 4, 5, 8, 9, 11} e  U₄ = {4, 5, 3.4, 5.9, 23, -13} dois conjuntos. Encontrar

a) U₃ È U₄;
b) U₃ Ç U₄;
c) juntar conjuntos U₃ e U₄;
d) complemento de U₃ com U₄;
e) complemento de U₄ com U₃.

Resolução

Inicialmente damos os seguintes comandos para definir os conjuntos U₃ e U₄:

In[ ]:= U3={-1, 3, -8, 4, 5, 8, 9, 11}
Out[ ]= {-1, 3, - 8, 4, 5, 8, 9, 11}

In[ ]:= U4={4, 5, 3.4, 5.9, 23, -13}
Out[ ]= {4, 5, 3.4, 5.9, 23, -13}

a) In[ ]:= Union[U3,U4]
     Out[ ]= {-13, -8, -1, 3, 3.4, 4, 5, 5.9, 8, 9, 11, 23}

b) In[ ]:= Intersection[U3,U4]
     Out[ ]= {4, 5}

c) In[ ]:= Join[U3,U4]
    Out[ ]= {-1, 3, -8, 4, 5, 5, 8, 9, 11, 4, 5, 3.4, 5.9, 23, -13}

d) In[ ]:= Complement[U3,U4]
     Out[ ]= {-8, -1, 3, 8, 9, 11}

e) In[ ]:= Complement[U4,U3]
     Out[ ]= {-13, 3.4, 5.9, 23}

Assim, concluímos que

• U₃ È U₄ = {-13, -8, -1, 3, 3.4, 4, 5, 5.9, 8, 9, 11, 23};
• U₃ Ç U₄ = {4, 5};
• conjuntos U₃ e U₄ junto é o conjunto {-1,3,-8,4,5,8,9,11,4,5,3.4,5.9, 23, -13};
• complemento de U₃ com U₄ é o conjunto {-8, -1, 3, 8, 9, 11};
• complemento de U₄ com U₃ é o conjunto {-13, 3.4, 5.9, 23}.

Os comandos utilizados são explicados a seguir:

• O comando "=" lista os elementos do conjunto.

• Os comandos "Max" e "Min" fornecem o valor máximo e mínimo do conjunto, respectivamente.

• Os comandos "Union", "Intersection" e "Complement" representam as operações união, intersecção e complementar entre os conjuntos dados, respectivamente.

• O comando "Union" ordena os elementos e retira os elementos repetidos.

•  O comando "Length" fornece o número de elementos no conjunto dado.

•  O comando "Join" é utilizado como "Union", porém com repetição dos elementos comuns.

1.7 Funções matemáticas

 O software Mathematica tem inúmeras funções matemáticas já definidas (embutidas). Algumas delas são dadas a seguir. Os nomes das funções predefinidas iniciam-se com letras maiúsculas e os argumentos de todas as funções em Mathematica são colocados entre colchetes [ ]. Por exemplo:

Sqrt[ ]           - raiz quadrada.

N[Sqrt[ ]]      - N é utilizado para ter resposta em decimais.

Sin[ ]             - função seno.

Cos[ ]            - função cosseno.

Tan[ ]            - função tangente.

E                    - exponencial natural.

Exp[ ]             - função exponencial.

N[Exp[ ]]        - valor em decimal.

Log[ ]              - função logarítmica natural.

Abs[ ]              - valor absoluto.

I                        - número complexo i =.

Pi                      - a letra grega p .

1.8 Números complexos

Os números complexos são representados na forma z = a + b i, com a e b Î e i² = -1, onde a é a parte real e b é a parte imaginária do número complexo. Veja alguns exemplos a seguir:

Exemplo 1.3

Seja z = 5 - 7 i  um número complexo. Encontrar

a) parte real de z;
b) parte imaginária de z;
d) complexo conjugado de z;
e) valor absoluto de z;
f) argumento de z.

Resolução

Veja os comandos a seguir:

a) In[ ]:= z = 5 - 7 I
     Out[ ]= 5 - 7 I

b) In[ ]:= Re[z]
     Out[ ]= 5

c) In[ ]:= Im[z]
    Out[ ]= -7

d) In[ ]:= Conjugate[z]
     Out[ ]= 5 + 7 I

e) In[ ]:= Abs[z]
    Out[ ]= Sqrt[74]

 f) In[ ]:= Arg[z]
    Out[ ]= -ArcTan[]

      In[ ]:= %//N
      Out[ ]= -0.950547

Assim, concluímos que

• parte real do número complexo z= 5 - 7 i é dada por 5;
• parte imaginária do número complexo z= 5 - 7 i é dada por - 7;
• complexo conjugado de z= 5 - 7 i é dada por 5 + 7 i;
• valor absoluto do número complexo z = 5 - 7 i é dado por ;
• argumento do número complexo z = 5 - 7 i é dado por - 0,950547.

Os comandos utilizados anteriormente têm suas explicações a seguir:

• Os comandos "Re[z]" e "Im[z]" calculam a parte real e a parte imaginária de um número complexo z, respectivamente.

• O comando "Conjugate[z]" calcula o conjugado de um número complexo z, isto é, calcula . 

• O comando "Abs[z]" calcula o valor absoluto (ou norma) de um número complexo z.

• O comando "Arg[z]" calcula o argumento de um número complexo representando o resultado (em radianos) com variação entre -p e p .

1.9 Computação algébrica e numérica

Podemos trabalhar com fórmulas algébricas e numéricas no software Mathematica. Ele nos permite escrever qualquer tipo de expressão algébrica. Estas expressões matemáticas envolvem variáveis e constantes. Faremos a seguir em quatro subseções as expressões, expansões, fatorações e simplificações.

1.9.1 Expressão

Em expressões algébricas, podemos efetuar as operações de adição, subtração, multiplicação, divisão e potenciação.

Exemplo 1.4

a) Escrever a expressão matemática x³ + 7x² - 4x - 5 nos comandos do Mathematica e calcule seu valor quando x = 2.

 b) Escrever a expressão matemática 2x⁴ y³ + 7xy - 12x³ y² e calcular seu valor quando

Resolução

Veja os comandos a seguir:

 a)  In[ ]:= x^3+7 x^2- 4 x- 5
      Out[ ]= - 5 - 4 x + 7 x² + x³

       In[ ]:= % /. x-> 2
       Out[ ]= 23

b)  In[ ]:= x y- 2 x^4 y^3+6 x y- 12 x^3 y^2
     Out[ ]= 7 x y - 12 x³ y² - 2 x⁴ y³

i)  In[ ]:= % /. x -> 1.5
    Out[ ]= 10.5 y - 40.5 y² - 10.125 y³

ii) In[ ]:= % /. y -> 2
     Out[ ]= -222.

Assim concluímos que

• valor da expressão x³ + 7x² - 4x - 5 no ponto x = 2 é 23;

• valor da expressão 7x y - 12x³ y² - 2x⁴ y³ no ponto x = 1,5 é 10,5 y - 40,5 y² - 10,125 y³ e no ponto x = 1,5 e y = 2 é - 222.

1.9.2 Expansão

O programa Mathematica desenvolve as expressões algébricas de forma parcial ou total, dependendo do comando utilizado. Vejamos alguns exemplos abaixo:

Exemplo 1.5

Expandir as seguintes expressões:

a) (1+x)³;
b) (x- 2)(x- 6)(x²- 2x+1).

Resolução

Veja os comandos a seguir:

a)  In[ ]:= Expand[(1+x)^3]
      Out[ ]= 1 + 3 x + 3 x² + x³

b)  In[ ]:= Expand[(x- 2)(x- 6)(x^2- 2 x+1)]
      Out[ ]= 12 -32 x + 29 x² -10 x³ + x⁴

Assim concluímos que

• (1+x)³ = 1 + 3 x + 3 x² + x³;

• (x- 2)(x- 6)(x^2- 2x+1) = 12 - 32 x + 29 x² - 10 x³ + x⁴.

O comando utilizado têm sua explicação a seguir:

•  O comando "Expand" expande as operações da expressão, reescrevendo-a.

1.9.3 Simplificação

Exemplo 1.6

Simplificar as seguintes expressões:

a) x² - 3x + 2;
b) (3 x+4)(4x- 3).

Resolução

Veja os comandos a seguir:

a)  In[ ]:= Simplify[x^2- 3 x+2]
     Out[ ]= 2 - 3 x + x²

b)  In[ ]:= Simplify[(3 x+4)(4x- 3)]
     Out[ ]= -12 + 7 x + 12 x²

Assim concluímos que

• x² -3x + 2 = x² -3x + 2;

• (3x + 4)(4x - 3) = - 12 + 7x + 12x².

O comando utilizado tem sua explicação a seguir:

• O comando "Simplify" opera da mesma forma que o comando "Expand".

1.9.4 Fatoração

 Para fatorar expressões algébricas utiliza-se o comando "Factor". Também utilizamos o comando "FactorInteger". Os exemplos a seguir são de fatoração de expressões e números.

Exemplo 1.7

Fatorar as seguintes expressões e números:

a) x³ +2x² - 1;
b) ;
c) 24 (em fatores primos);
d) 30! e escrever em fatores primos.

Resolução

Veja os comandos a seguir:

a)  In[ ]:= Factor[x^3+2 x^2-1]
       Out[ ]= (1 + x)(-1 + x + x²)

 b) In[ ]:= Factor[x^3+(5 x^2)/6 - 2 x+2/3]
        Out[ ]=

c)  In[ ]:= FactorInteger[24]
       Out[ ]= {{2,3}, {3,1}} (isto é, 2³ 3¹, fatores primos)

d)  In[ ]:= 30!
       Out[ ]= 265252859812191058636308480000000

        In[ ]:= 30!//N
        Out[ ]= 2.65253 10³²

        In[ ]:= FactorInteger[%%]
        Out[ ]= {{2,26},{3,14},{5,7},{7,4},{11,2},{13,2}, {17,1},{19,1},{23,1},{29,1}}

Assim, concluímos que

• x³ +2x² - 1 = (1 + x)(- 1 + x + x²);

• = ;

• 24 = 2³ 3¹;

• 30! = 265.253 ´ 10³² = 2²⁶ 3¹⁴ 5⁷ 7⁴ 11² 13² 17¹ 19¹ 23¹ 29¹.

Os comandos utilizados têm suas explicações a seguir:

• O comando "Factor" fornece a expressão na sua forma irredutível (fatorada).

• O comando "FactorInteger" fatora inteiros, fornecendo os fatores primos com seus respectivos expoentes.

1.10 Divisão de polinômios

A seguir apresentamos alguns exemplos de divisão de um polinômio por outro polinômio de menor grau.

Exemplo 1.8

Utilizar Mathematica para dividir os seguinte polinômios:

a) x⁴ + 3x² - 1 por x³ + x;
b) 3x² + x - 4 por 2x + 1.

Resolução

Para resolver estes exemplos, utilizamos os comandos "PolynomialRemainder", "PolynomialQuotient" e "Simplify". O comando "Simplify" foi utilizado para tirar a prova real da divisão.

a)  In[ ]:= PolynomialRemainder[x^4+3 x^2- 1,x^3+x,x]
      Out[ ]= -1 + 2 x²

      In[ ]:= PolynomialQuotient[x^4+3 x^2- 1,x^3+x,x]
      Out[ ]= x

      In[ ]:= Simplify[(x^3+x)% + %%]
      Out[ ]= -1 + 3 x² + x⁴

b)  In[ ]:= PolynomialRemainder[3 x^2+x- 4,2 x+1,x]
      Out[ ]= - ()

       In[ ]:= PolynomialQuotient[3 x^2+x- 4,2 x+1,x]
       Out[ ]=

        In[ ]:= Simplify[(2 x+1)% + %%]
        Out[ ]= -4 + x + 3 x²

 Assim, concluímos que

• x⁴ + 3x² - 1 = (x³ +x) x +(x⁴ + 3 x² - 1);

• 3x² + x - 4 =(2x + 1) () - ().

Os comandos usados têm suas explicações a seguir:

•  O comando "PolynomialRemainder[p(x),q(x),x]" fornece o resto da divisão de um polinômio p(x) por q(x).

•  O comando "PolynomialQuotient[p(x),q(x),x]" fornece o quociente da divisão do polinômio p(x) por q(x).

Exemplo 1.9

Encontrar as frações parciais das expressões:

a) u₁ = 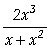, x ¹ 0;
b) u₂ = .

Resolução

Utilizamos os comandos a seguir para resolver este exemplo:

a)  In[ ]:= u1=2x^3/(x^2+x)
      Out[ ]=

        In[ ]:= Factor[u1]
        Out[ ]=

        In[ ]:= Apart[u1]
        Out[ ]= -2 + 2 x +

 b)  In[ ]:= u2=(2x+1)/(2x^2+3x-2)
         Out[ ]=

         In[ ]:= Factor[u2]
         Out[ ]=

         In[ ]:= Apart[u2]
         Out[ ]=

         In[ ]:=Together[u2]
         Out[ ]=

 Assim concluímos que

• = ;

• =.

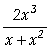Os comandos utilizados têm suas explicações a seguir:

• O comando "Factor" foi utilizado anteriormente e funciona para fatorar a expressão dada.

• O comando "Together" também foi utilizado anteriormente e funciona para juntar expressões já fatoradas parcialmente.

• O comando "Apart" é utilizado para decompor uma fração em frações parciais.

• O comando "Cancel" é utilizado para cancelar fatores comuns em numerador e denominador do mesmo quociente.

1.11.1 Frações parciais em duas variáveis

Nesta subseção apresentamos um exemplo de frações parciais envolvendo duas funções com várias opções.

Exemplo 1.10

 Encontrar as frações parciais da expressão dada em duas variáveis:

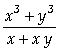a) em relação a x;
b) em relação a y.

Resolução

Utilizamos os seguintes comandos para achar as frações parciais:

In[ ]:= v1=(x^3+y^3)/(x+x y)
Out[ ]=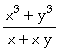

In[ ]:= Factor[v1]
Out[ ]=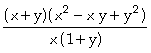

a) Em relação a x

In[ ]:= Apart[v1,x]
Out[ ]=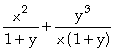

b) Em relação a y

In[ ]:= Apart[v1,y]
Out[ ]=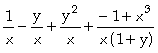

 Assim concluímos que

• as frações parciais em relação a x são dadas por

• as frações parciais em relação a y são dadas por

1.12 Funções

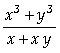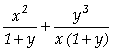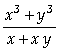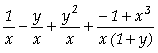O Mathematica tem uma série de comandos que tratam das funções. Para representar as funções utilizamos os sinais "_" e ":=". O sinal "_" é usado no lado esquerdo para indicar os argumentos da função, o sinal ":=" é usado em vez de "=". Aqui seguem alguns exemplos.

Exemplo 1.11

a) Seja f(x) = x³. Encontrar

       i) f(3);
       ii) f(5,9);
       iii) f(a) + f(a- 1) + 3 f(a²).

b) Seja h(x,y) = . Encontrar

      i) h(3,4);
      ii) h(2.4,5.3).

Resolução

Veja os comandos a seguir:

a)  In[ ]:= f[x_]:= x^3

i)  In[ ]:= f[3]
    Out[ ]= 27

ii) In[ ]:= f[5.9]
     Out[ ]= 205.379

iii) In[ ]:= f[a]+f[a-1]+3 f[a^2]
       Out[ ]= (- 1+a)³ + a³ + 3 a⁶

Assim concluímos que

• f(3) = 27;

• f(5,9) = 205,379;

• f(a) + f(a-1) + 3 f(a²) = (- 1+a)³ + a³ + 3 a⁶.

b)  In[ ]:= h[x_, y_]:= Sqrt[x^2+y^2]

i)  In[ ]:= h[3,4]
     Out[ ]= 5

ii)  In[ ]:= h[2.4,5.3]
      Out[ ]= 5.81808

Assim, concluímos que

• h(3,4) = 5;

• h(2.4,5.3) = 5, 81808.

1.12.1 Funções compostas

Dadas duas funções f e g, chama-se função composta de f com g a função definida por f(g(x)). Simbolicamente escrevemos:

O Mathematica trabalha com as funções compostas. Os exemplos a seguir calculam as funções compostas definidas acima. Também utilizamos os comandos "Composition" e "Nest", em relação à composição das funções.

Exemplo 1.12

Sejam as funções definidas por:

f(x) = x³;
g(x) = log₁₀ x³;
h(x) = sin(3x) cos(x);
k(x) = x² - 4x + 3.

Encontrar

a) f(g(x);
b) f(g(h(k(x))));
c) k(g(f(x)));
d) f(f(f(x)));
e) g(g(x));
f) h(h(x)).

Resolução

Inicialmente definimos as funções dadas dando os seguintes comandos:

In[ ]:= Clear[f,g,h,k]

f[x_] := x^3
g[x_] := Log[x^3]
h[x_] := Sin[3x] Cos[x]
k[x_] := x^2-4 x+3

Para encontrar as composições solicitadas, aplicamos os comandos "Composition" e "Nest". Veja a seguir:

a)  In[ ]:= Composition[f,g][x]
      Out[ ]= Log[x³]³

b)  In[ ]:= Composition[f,g,h,k][x]
      Out[ ]= Log[Cos[3 - 4 x + x²]³ Sin[3(3 - 4 x + x²)]³]³

c)   In[ ]:= Composition[k,g,f][x]
      Out[ ]= 3 - 4 Log[x⁹] + Log[x⁹]²

d)  In[ ]:= Nest[f,x,3]
      Out[ ]= x²⁷

e)   In[ ]:= Nest[k,x,2]
       Out[ ]= 3 - 4(3 - 4 x + x²)+(3 - 4 x + x²)²

f)    In[ ]:= Nest[h,x,2]
       Out[ ]= Cos[Cos[x] Sin[3x]] Sin[3 Cos[x] Sin[3x]]

 Assim, concluímos que

• f(g(x) = log(x³)³;

• f(g(h(k(x)))) = log(cos(3 - 4x + x²)³ sen(3(3 - 4 x + x²))³)³;

• k(g(f(x)))= 3 - 4 log(x⁹) + log(x⁹)²;

• f(f(f(x)))= x²⁷;

• g(g(x))= 3 - 4(3 - 4 x + x²)+(3 - 4 x + x²)²;

• h(h(x))= cos(cos(x) sen(3x)) sen(3 cos(x) sen(3x)).

Os comandos utilizados têm suas explicações a seguir:

• A representação de função é da forma "f[x_]:=" ou "h[x_, y_]:=". Esta representação é diferente da representação de conjuntos, "=", explicada anteriormente.

• O comando "Clear" apaga da memória a função definida anteriormente com a mesma representação.

• O comando "Composition" é equivalente à composição das funções f[g[h[k[x]]]], e depende do número de funções utilizadas na composição.

• O comando "Nest[f,x,2]" significa a composição f[f[x]], isto é, composição de f com f duas vezes. Observe que o comando "Composition" compõe funções quaisquer, enquanto que o comando "Nest" compõe uma função com ela mesma.