

Resolução de equações
Nesta subseção apresentamos resoluções de equações utilizando os comandos do software Mathematica. Também apresentamos resoluções de sistema de equações de duas e três variáveis. O principal comando utilizado é o "Solve". Utilizando o comando "Plot", mostramos algumas soluções destas equações no sistema cartesiano. Veja a seguir alguns exemplos.
Exemplo 3.1
Achar soluções das seguintes equações e represente-as graficamente:
a) 5x -
12 = 0;
b) x2 -
5x - 6 = 0;
Resolução
Utilizamos o comando "Solve" para resolver estes exemplos. Logo aplicamos o comando "Plot" para construir os gráficos das equações dadas para visualizar melhor os pontos de interseção. Veja os comandos seguir:
a) In[
]:= Solve[5 x-
12==0,x]
Out[
]= {{x -> ![]() }}
}}
In[ ]:= Plot[5 x- 12,{x,- 3,3}]
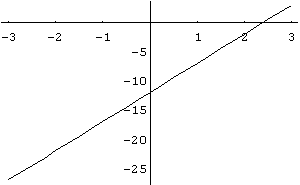
Out[ ]= -Graphics-
b)
In[ ]:= Solve[x^2-
5 x- 6==0,x]
Out[
]= {{ x -> -
1}, { x -> 6}}
In[ ]:= Plot[x^2- 5 x- 6,{x,- 2,7}]
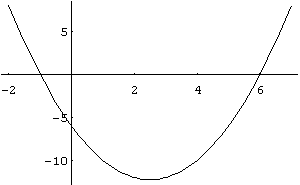
Out[ ]= -Graphics-
Observação
Observe que a colocação de x dentro do comando não é obrigatória quando resolvemos a equação de apenas uma variável. Se trabalhamos com função composta ou com duas ou mais variáveis é necessário colocar estas variáveis, conforme a situação. Veja os exemplos a seguir:
Exemplo 3.2
Resolver as equações cos2x - 3 cos x + 2 = 0 e representar graficamente:
Resolução
O comando "Solve[Cos[x]^2- 3 Cos[x]+2==0]" resolve equação em termos da função cos x, em vez de x.
In[
]:= Solve[Cos[x]^2-3 Cos[x]+2==0]
Out[ ]= {{Cos[x] ->
1}, {Cos[x] -> 2}}
O comando "Solve[Cos[x]^2- 3 Cos[x]+2==0,x]" resolve a equação para x e utiliza a função inversa.
In[ ]:=
Solve[Cos[x]^2-3 Cos[x]+2==0,x]
Out[ ]= {{x
-> 0}, {x -> ArcCos[2]}}
In[
]:= Solve[Cos[x]^2-
3 Cos[x]+2==0,x]//N
Out[ ]=
{{x -> 0}, {x -> 1.31696 I}}
In[ ]:= Plot[Cos[x]^2- 3 Cos[x]+2,{x,- 2,13}]
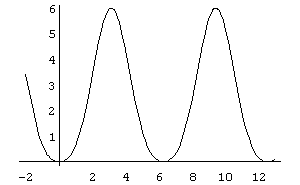
Out[ ]= -Graphics-
A seguir, veja mais exemplos de resolução de equações.
Exemplo 3.3
Resolver as seguintes equações e represente-as graficamente:
a) x6 -
1 = 0;
b) x4 - 3x3 -
11x2 + 3x + 10 = 0.
Resolução
a) In[
]:= Solve[x^6-
1==0,x]
Out[
]= {{x-> 1},{x->(-
1)1/3},{x->(-
1)2/3},{x->-
1},{x->(-
1)4/3},{x->(-
1)5/3}}
In[
]:= %//N
Out[ ]=
{{x-> 1.},{x-> 0.5 + 0.866025 I},{x-> -0.5
+ 0.866025 I},{x-> -1.},
{x->
0.5 -0.866025 I},{x-> 0.5 -0.866025
I}}
In[ ]:= Plot[x^6- 1,{x,- 2,2}]
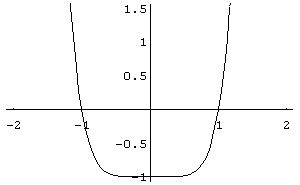
Out[ ]= -Graphics-
b) In[
]:= Solve[x^4-
3x^3- 11x^2+3x+10==0,x]
Out[
]= {{x -> -
2}, {x -> - 1}, {x -> 1}, {x -> 5}}
In[ ]:= Plot[x^4- 3x^3- 11x^2+3x+10,{x,- 4,7}]
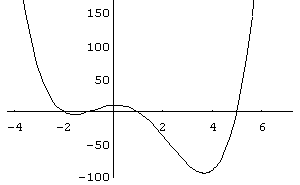
Out[ ]= -Graphics-
Observação
Exemplo 3.4
Resolver a equação 12x5 + x4 + 19x3 - 18x2 - 3x + 3 = 0.
Resolução
Para resolver estes exemplos veja os comandos utilizados a seguir:
In[
]:= Solve[12 x^5+x^4+19 x^3-
18 x^2- 3 x+3==0,x]
Out[ ]=
{ToRules[Roots[- 3 x -
18 x2 + 19 x3 + x4 + 12 x5
== - 3, x]]}
Aplicando o comando "Solve" na equação dada não obtemos as soluções. Para resolvê-la, aplicamos a seguir o comando "Nroots" ou o comando "Solve" com a opção "//N":
In[
]:= NRoots[12 x^5+x^4+19 x^3-
18 x^2- 3 x+3==0,x]
Out[ ]=
x == - 0.400308 || x == -
0.376689 - 1.44761 I ||
x == -
0.376689 + 1.44761 I || x == 0.449755 ||
x == 0.620597,
ou
In[
]:= Solve[12 x^5+x^4+19 x^3-
18 x^2- 3 x+3==0,x]//N
Out[ ]=
{{x -> - 0.400308},{x ->
- 0.376689 - 1.44761
I},
{x -> -
0.376689 + 1.44761 I}, {x -> 0.449755}, {x -> 0.620597}}
Aplicando o comando "NRoots" ou "//N" após a expressão com o comando "Solve" achamos as raízes do polinômio de 5o grau, sendo que três delas são números reais e duas são números complexos.
Exemplo 3.5
Sejam f(x) e g(x) funções definidas por:
f(x) = x2 + 4x - 5 e g(x) = 3x2 + x/4 - 12.
Achar as soluções aproximadas da equação f(x) = g(x) e represente-as graficamente.
Resolução
Resolvemos os exemplos utilizando os comandos "NSolve" ou "NRoots". Os dois comandos produzem o mesmo resultado. Para esboçar os gráficos utilizamos o comando "Plot".
a) In[
]:= Clear[f,g]
f[x_]:=x^2+4
x- 5
g[x_]:=3
x^2+x/4- 12
NSolve[f[x]==g[x],x]
Out[ ]= {{x -> -1.15508}, {x -> 3.03008}}
ou
In[
]:= NRoots[f[x]==g[x],x]
Out[ ]=
x == -1.15508 || x == 3.03008
In[ ]:= Plot[{f[x],g[x]},{x,- 7,7}, PlotStyle->{GrayLevel[0],GrayLevel[0.5]}]

Out[ ]= -Graphics-
Observações
3.2 Resolução de sistema de equações
Nesta subseção, daremos exemplos de resolução de sistema de equações.
Exemplo 3.6
Resolver o seguinte sistema de equações e representar as soluções graficamente:
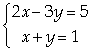
Resolução
Utilizamos o comando "Solve" para resolver estes sistema de equações:
In[ ]:= Solve[{2 x- 3 y==5,x+y==1},{x,y}]
Out[
]= {{ x ->![]() ,
y ->
,
y -> ![]() }}
}}
Para representar graficamente, primeiro resolvemos as equações para y e depois aplicamos o comando "Plot" para traçar as duas retas simultaneamente.
In[ ]:= Solve[2x- 3y==5,y]
Out[
]= {{y -> ![]() }}
}}
In[
]:= Solve[x+y==1,y]
Out[ ]= {{y
-> 1 - x}}
Podemos também, resolver as equações simultaneamente em termos de uma variável x ou y, dando o seguinte comando:
In[
]:= Solve[2x-
3y==5||x+y==1,y]
Out[ ]=
{{y -> 1 - x},{y ->
![]() }}
}}
In[ ]:= Plot[{1- x,( - 5+2x)/3},{x, - 3,3}]
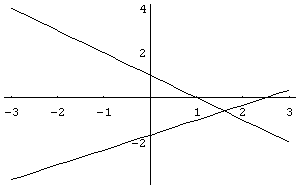
Out[ ]= -Graphics-
Exemplo 3.7
Resolver o seguinte sistema de equação:
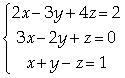
Resolução
Utilizamos o comando "Solve" para resolver estes sistemas de equações:
In[
]:= Solve[{5 x-3
y+2 z==6,4 x-2 y+3 z==-1,
x+2 y-z==2},{x,y,z}]
Out[ ]=
{{ x ->![]() ,
y ->
,
y ->![]() , z
->
, z
-> ![]() }}
}}
A seguir apresentamos exemplos de sistema de equações com soluções infinitas.
Exemplo 3.8
Resolver o seguinte sistema de equações:
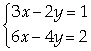
Resolução
In[
]:= Solve[{3 x-
2 y==1,6 x- 4 y==2},{x,y}]
Out[ ]=
{{x -> ![]() }}
}}
Observamos que as soluções dos sistemas resolvidos acima são infinitas.
3.3 Curvas passando por pontos dados
Nesta subseção encontraremos as curvas que passam por pontos dados.
Exemplo 3.9
a) Sejam os pontos (- 3,2) e (5,4) no plano cartesiano. Queremos encontrar a reta que passa por estes pontos;
b) Sejam os pontos (1,1), (2,0) e (3,2) no plano cartesiano. Queremos encontrar a parábola que passa por estes pontos;
c) Sejam os pontos (1,2), (- 2,3), (2,1) e (3,- 2) no plano cartesiano. Queremos encontrar a curva da função cúbica que passa por estes pontos.
Resolução
a) Teremos que determinar a função linear f(x) = ax + b que passa pelos pontos (- 3,2) e (5,4). Isto é, a função f(x) deve satisfazer as equações f(- 3) = 2 e f(5) = 4. Temos duas equações envolvendo a e b: f(- 3) = - 3a + b = 2 e f(5) = 5a + b = 4. Resolvemos estas equações utilizando o comando "Solve".
In[
]:= Clear[f,a,b]
f[x_] := a x+b
Solve[{f[-
3]==2,f[5]==4},{a,b}]
Out[ ]=
{{a -> ![]() ,
b ->
,
b -> ![]() }}
}}
In[ ]:= Plot[1/4 x+11/4,{x,- 4,6}]
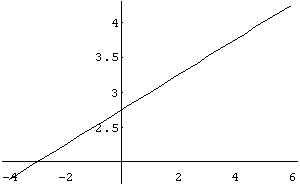
Out[ ]= -Graphics-
Observamos através do gráfico que a função obtida passa pelos pontos dados
b) Teremos que determinar a função quadrática f(x) = ax2 + bx + c que passa pelos pontos (1,1), (2,0) e (3,2). Isto é, a função f(x) deve satisfazer as equações f(1) = 1, f(2) = 0 e f(3) = 2. Estamos diante de três equações envolvendo a, b e c:
f(1) = a + b
+ c = 1,
f(2) = 4a + 2b + c = 0,
f(3) = 9a + 3b + c = 2.
Resolvemos estas equações utilizando o comando "Solve".
In[ ]:=
Clear[f,a,b,c]
f[x_]:=a x^2+b x+c
Solve[{f[1]==1,f[2]==0,f[3]==2},{a,b,c}]
Out[ ]= {{ a -> ![]() ,
b -> -(
,
b -> -(![]() ),
c -> 5}}
),
c -> 5}}
Vamos construir o gráfico da função obtida para verificação.
In[ ]:= Plot[3/2 x^2- 11/2 x+5,{x,- 1,4}]
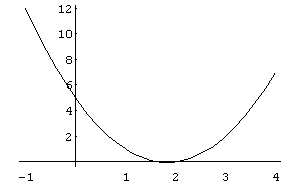
Out[ ]= -Graphics-
Observamos que a curva passa pelo pontos dados. Para se ter mais clareza próximo do ponto 2, isto é, na interseção da curva com o eixo x, vamos construir um outro gráfico diminuindo o intervalo no eixo x.
In[ ]:= Plot[3/2 x^2- 11/2 x+5,{x,1.5,2.5}]
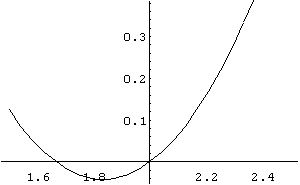
Out[ ]= -Graphics-
c) Teremos que determinar a função cúbica f(x) = ax3 + bx2 + cx + d que passa pelos pontos (1,2), (-2,3), (2,1) e (3,-2). Isto é, a função f(x) deve satisfazer as equações f(1) = 2, f(- 2) = 3 e f(2) = 1 e f(3) = - 2. Resolvemos estas equações utilizando o comando "Solve".
In[
]:= Clear[f,a,b,c,d]
f[x_]:=a x^3+b x^2+c x+d
Solve[{f[1]==2,f[-
2]==3,f[2]==1,f[3]==- 2}, {a,b,c,d}]
Out[ ]=
{{a -> - (![]() ),
b -> 0, c ->
),
b -> 0, c -> ![]() ,
d -> 2}}
,
d -> 2}}
Vamos construir o gráfico da função obtida.
In[ ]:= Plot[- 1/6 x^3+1/6 x+2,{x,- 3,4}]
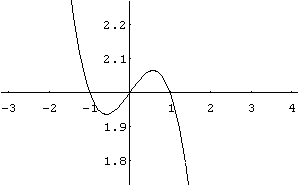
Out[ ]= -Graphics-
3.4 Resolução das equações por aproximação gráfica
Nesta seção, apresentamos alguns exemplos de sistemas de equações que não são fáceis de resolver por simplificações. Neste caso vamos resolvê-los através de representações gráficas.
Exemplo 3.10
Achar as coordenadas dos pontos de intersecção das curvas y = cos 3x + 3 e y = 4 - x2 apresentando o resultado com até três decimais.
Resolução
Inicialmente damos o comando "Solve" e vemos que desta forma não é possível achar a solução.
In[
]:= Solve[{Cos[3x]-y==-3,
y+x^2==4}, {x,y}]
Out[ ]=
Solve[{-
y + Cos[3 x]== -
3, x2 + y== 4},{x,y}]
Resolvemos então o sistema de equações, traçando uma seqüência de gráficos das funções simultaneamente.
In[ ]:= Plot[{Cos[3x]+3,4- x^2},{x,- 3,3}]
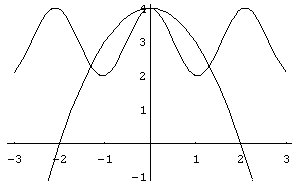
Out[ ]= -Graphics-
In[ ]:= Plot[{Cos[3x]+3,4- x^2},{x,1,2}]
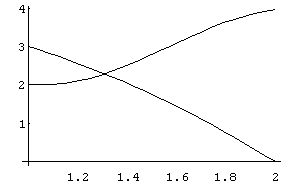
Out[ ]= -Graphics-
In[ ]:= Plot[{Cos[3x]+3,4- x^2},{x,1.25,1.35}]
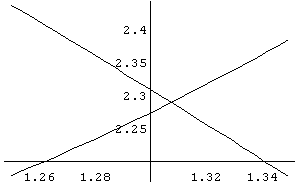
Out[ ]= -Graphics-
In[ ]:= Plot[{Cos[3x]+3,4- x^2},{x,1.3,1.31}]
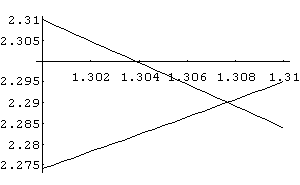
Out[ ]= -Graphics-
In[ ]:= Plot[{Cos[3x]+3,4- x^2},{x,1.307,1.308}]
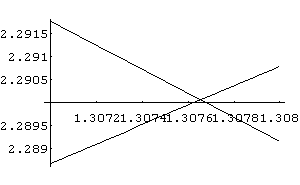
Out[ ]= -Graphics-
In[ ]:= Plot[{Cos[3x]+3,4- x^2},{x,1.307,1.308}, PlotRange->{2.2895,2.2905}]
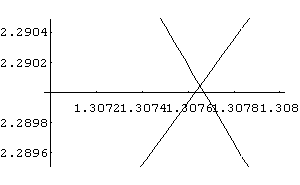
Out[ ]= -Graphics-
Através das aproximações dos gráficos em relação ao intervalo dos eixos concluímos que os pontos de interseção das equações são:
{x = 0,y = 4}, {x = 1.307, y = 2.290} e {x = - 1.307, y = 2.290}
Exemplo 3.11
Achar as coordenadas dos pontos de interseção das curvas
y = 2 sen x + 3 cos x e y = x2 - 3x.
Resolução
Inicialmente damos o comando "Solve" e vemos que desta forma não é possível achar a solução.
In[
]:= Solve[{y==2 Sin[x]+3 Cos[x],y==x^2-
3 x},{x,y}]
Out[ ]=
Solve[{y==3 Cos[x]+2 Sin[x],y==-
3 x +x2},{x,y}]
Vamos resolver então o sistema de equações, traçando uma seqüência de gráficos das funções simultaneamente.
In[ ]:= Plot[{2 Sin[x]+3 Cos[x],x^2- 3 x},{x,- 10,10}]
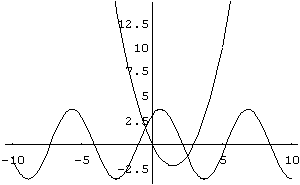
Out[ ]= -Graphics-
No gráfico acima vemos que as equações dadas têm duas soluções reais, isto é, têm dois pontos de interseção. Vamos analisar estes pontos, um de cada vez.
In[ ]:= Plot[{2 Sin[x]+3 Cos[x],x^2- 3 x},{x,2,3}]
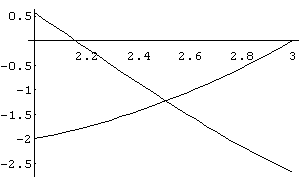
Out[ ]= -Graphics-
In[ ]:= Plot[{2 Sin[x]+3 Cos[x],x^2 - 3 x},{x,2.4,2.6},PlotRange->{- 1.5,- 1}]
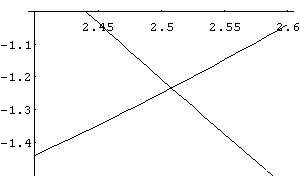
Out[ ]= -Graphics-
In[ ]:= Plot[{2 Sin[x]+3 Cos[x],x^2- 3 x}, {x,2.50,2.51}, PlotRange->{-1.24,-1.22}]
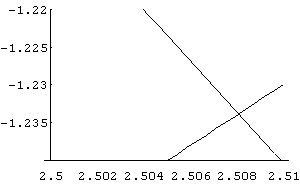
Out[ ]= -Graphics-
In[ ]:= Plot[{2 Sin[x]+3 Cos[x],x^2- 3 x}, {x,- 2.5,0},PlotRange->{0,2.5}]
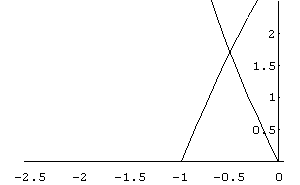
Out[ ]= -Graphics-
In[ ]:= Plot[{2 Sin[x]+ 3 Cos[x],x^2- 3 x},{x,- 1,- 0.4},PlotRange->{1.5,2}]
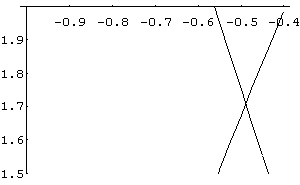
Out[ ]= -Graphics-
Através das aproximações dos gráficos em relação ao intervalo dos eixos, concluímos que os pontos de intersecção das equações são:
{ x = 2.508, y = - 1.234 } e { x = - 0.5, y = 1.7 }
Observações