4.1 Introdução

O conceito de limite e continuidade é um conceito importante na definição de derivada e integral. Neste capítulo trabalhamos com limite, continuidade, derivada e integral utilizando os comando do Mathematica. Abordamos também a derivada de ordem superior, derivada parcial, derivada das funções implícitas e integração múltipla.

4.2 Conceito de limite

Iniciamos este capítulo com o cálculo de limites. O comando utilizado em Mathematica para este cálculo é "Limit[expressão,x->x₀]". Também utilizamos a opção "Direction", o que permite o cálculo de limites laterais, isto é, à direita e à esquerda. Veja os exemplos a seguir:

Exemplo 4.1

Calcular os seguinte limites:

a) , onde ;

b) ;

c) , onde f(x) é dada como em a).

Resolução

Utilizamos o comando "Limit" para resolver estes exemplos:

a)  In[ ]:= f[x_]:=(- 5+3 x+4 x^2)/(10- 5 x+8 x^2)
           Limit[f[x],x->5]
     Out[ ]=

b) In[ ]:= Limit[(1+x)^(1/x),x->0]
     Out[ ]= E

c) In[ ]:= Limit[f[x],x->Infinity]
     Out[ ]=

Assim, concluímos que

• = ;
• = e;
• =.

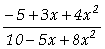A seguir apresentamos exemplos de cálculo de limites à direita e à esquerda.

Exemplo 4.2

Calcular os seguintes limites à direita e à esquerda:

a) ;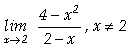
b) .

Faça a visualização gráfica de cada uma destas funções.

Resolução

Para calcular os limites direcionados utilizamos a opção "Direction" juntamente com o comando "Limit":

a) In[ ]:= f[x_]:=(4- x^2)/(2- x)

     In[ ]:= Limit[f[x],x->2,Direction-> -1]
     Out[ ]= 4

      In[ ]:= Limit[f[x],x->2,Direction->1]
      Out[ ]= 4

Assim, concluímos que

• ;

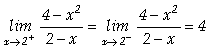isto é,

• .

Veja a seguir, o gráfico da função dada:

In[ ]:= Plot[(4- x^2)/(2- x),{x,0,3}]

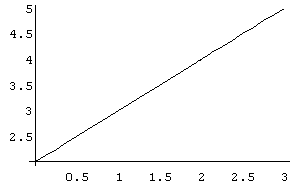
Out[ ]= -Graphics-

b) In[ ]:= Limit[1/x,x->0,Direction-> -1]
     Out[ ]= Infinity

    In[ ]:= Limit[1/x,x->0,Direction-> 1]
    Out[ ]= -Infinity

Assim, concluímos que

• e

isto é,

não existe.

A visualização gráfica desta função é obtida usando o comando "Plot".

In[ ]:= Plot[1/x,{x,- 1,1}]

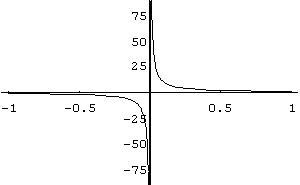
Out[ ]= -Graphics-

Observamos no gráfico acima que o limite da função no ponto x = 0 não existe.

O exemplo a seguir nos leva a definir o conceito de derivada utilizando o aspecto de limite.

Exemplo 4.3

Calcular , onde

a) f₁(x) = 4x³ 2x² - x 3;
b) f₂(x) = .

Resolução

Utilizamos os seguintes comandos para calcular os limites desejados:

a) In[ ]:= Clear[f1]
            f1[x_]:=4 x^3+2 x^2- x+3

     In[ ]:= k1=Simplify[(f1[x+h]- f1[x])/h]
     Out[ ]= -1+2 h + 4 h² + 4 x + 12 h x + 12 x²

      In[ ]:= Limit[k1,h->0]
     Out[ ]= -1 + 4 x + 12 x²

b)  In[ ]:= Clear[f2]
             f2[x_]:=(x^2+1)/x 

      In[ ]:= k2=Simplify[(f2[x+h]-f2[x])/h]
      Out[ ]=

       In[ ]:= Limit[k2,h->0]
       Out[ ]=

Assim, concluímos que

• ;

• .

O exemplo acima nos leva a definir o conceito de derivada de uma função, o que veremos na próxima seção.

4.3 Cálculo diferencial

 Seja uma função diferenciável f(x), isto é, que tem derivada, definida por

O Mathematica poderá computar sua derivada de pelo menos duas formas, desde que a função f(x) tenha sido definida de maneira adequada. Inicialmente calculamos a derivada usando a definição.

Seguem abaixo alguns comandos para se calcular derivadas:

• O comando "f’[x]" computa a derivada de f(x) em relação a x. 

• O comando "D[f[x],x]" também computa a derivada de f(x) e relação a x.

•  O comando "D[f[x],{x,n}]" computa a n-ésima derivada de f(x) em relação a x.

•  O comando "D[expressão,variável]" computa a derivada da expressão em relação a variável.

Exemplo 4.4

Calcular a derivada da expressão 7x - 9x² 8x³.

Resolução

Para se calcular a derivada da expressão 7x - 9x² + 8x³, podemos derivar diretamente ou podemos definir uma função f(x) = 7x - 9x² + 8x³. Os comandos abaixo calculam a derivada da mesma função de três formas diferentes:

1^a forma

In[ ]:= D[7 x- 9 x^2+8 x^3,x]
Out[ ]= 7 - 18 x + 24 x²

2^a forma

In[ ]:= Clear[h]
        h[x_]:=7 x- 9 x^2+8 x^3

In[ ]:= h'[x]
Out[ ]= 7 - 18 x + 24 x²

3^a forma

In[ ]:= D[h[x],x]
Out[ ]= 7 - 18 x + 24 x²

Observe que tanto "h’[x]" quanto "D[h[x],x]" produziram o mesmo resultado.

Assim, concluímos que

• (7x - 9x² 8x³)¢ = 7 - 18x 24x².

Exemplo 4.5

Calcular a derivada das seguintes funções

a) f(x) = x² sen x;
b) f(x) = ln(3x⁴ 4);
c) f(x) = (5x 3)(2x³ - 3x 4)².

Resolução

Resolvemos estes exemplos utilizando os comando "D" dado no exemplo acima.

a) In[ ]:= D[x^2 Sin[x],x]
     Out[ ]= x² Cos[x] + 2 x Sin[x]

b) In[ ]:= D[Log[3 x^4 + 4],x]
     Out[ ]=

c) In[ ]:= D[(5 x+3)(2 x^3- 3 x+4),x]
     Out[ ]= (3 + 5 x)(- 3 + 6 x²) + 5(4 - 3 x + 2 x³)

Assim, concluímos que

•  (x² sen x)¢ = x² cos(x) 2x sen(x);
• (ln(3x⁴ 4))¢ = ;
• ((5x 3)(2x³ - 3x 4)²)¢ = (3 5x)(- 3 6x²) 5(4 - 3x 2x³).

Exemplo 4.6

Calcular f¢ (x), f¢ ¢ (x) e f¢ ¢ ¢ (x) para as seguintes funções:

a) f(x) = x⁴ - 3x³ 5x² 3x1;
b) f(x) = .

Resolução

Utilizamos os seguintes comandos para resolver estes exemplos:

a) In[ ]:= Clear[f]
            f[x_]:= x^4- 3 x^3+5 x^2+3 x+1

     In[ ]:= D[f[x],x]
     Out[ ]= 3 + 10 x - 9 x² + 4 x³

      In[ ]:= D[f[x],{x,2}]
      Out[ ]= 10 - 18 x + 12 x²

      In[ ]:= D[f[x],{x,3}]
      Out[ ]= -18 + 24 x

Assim, concluímos que

• f¢ (x) = 3 10x - 9x² 4x³;
• f¢ ¢ (x) = 10 - 18x 12x²;
• f¢ ¢ ¢ (x) = - 18 24x.

b) In[ ]:= Clear[f]
            f[x_]:=(Sin[4 x])/x

      In[ ]:= D[f[x],x]
      Out[ ]=

       In[ ]:= D[f[x],{x,2}]
       Out[ ]=

       In[ ]:= D[f[x],{x,3}]
       Out[ ]=

Assim, concluímos que

• f¢ (x) = ;
• f¢ ¢ (x) = ;
• f¢ ¢ ¢ (x) = .

4.3.1 Derivadas da função implícita

Utilizando os comandos do Mathematica podemos calcular a derivada da função implícita f(x,y) = 0. Os principais comandos são os seguintes:

• O comando "Dt[equação,x]" computa a diferencial em relação a variável x.

•  A expressão encontrada durante a computação representa a derivada de y em relação a x, isto é, "Dt[expressão,variável]" computa a derivada total.

•  "Dt[expressão]" computa a diferencial total "d(expressão)".

Veja os exemplos a seguir, sobre os cálculos de derivadas das funções implícitas. A expressão "Dt[y,x]", encontrada durante a computação, representa a derivada de y em relação a x, isto é, Dt[y,x] = . Utilizamos o comando "Solve" para encontrar os resultados desejados.

Exemplo 4.7

Calcular para as funções implícitas dadas a seguir:

a) x² y² = 4;
b) .

Resolução

Resolvemos estes exemplos utilizando os seguintes comandos:

a) In[ ]:= Dt[x^2+y^2==4,x]
     Out[ ]= 2 x + 2 y Dt[y, x] == 0

      In[ ]:= Solve[Dt[x^2+y^2==4,x],Dt[y,x]]
      Out[ ]= {{Dt[y, x] -> - ()}}

b) In[ ]:= Solve[Dt[Exp[- (x^2+y^2)]==Log[x],x],Dt[y,x]]
     Out[ ]= {{Dt[y, x] -> }}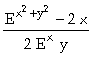

Os mesmos resultados acima, podem ser obtidos utilizando o comando "D" do Mathematica se declararmos que y é uma função de x, isto é, se escrevemos y=y[x]. Veja os cálculos abaixo:

a)  In[ ]:= D[x^2+y[x]^2==4,x]
      Out[ ]= 2 x + 2 y[x] y'[x] == 0

       In[ ]:= Solve[D[x^2+y[x]^2==4,x],y'[x]]
       Out[ ]= {{y'[x] -> - ()}}

b)  In[ ]:= Solve[D[Exp[- (x^2+y[x]^2)]==Exp[- x],x],y'[x]]
       Out[ ]= {{y'[x] -> }}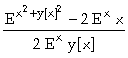

Assim, concluímos que

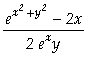• , onde x² y² = 4;
• , onde .

4.3.2 Derivada parcial

Derivadas parciais são calculadas utilizando o mesmo comando que foi utilizado para calcular a derivada, isto é, "D" ou "Derivative". Seja f(x,y) uma função diferenciável em relação às variáveis x e y. Utilizamos os seguintes comandos para os cálculos das derivadas parciais.

• O comando "D[f(x,y),variável]" computa a derivada parcial de f(x,y) em relação a variável x ou y.

• O comando "D[f(x,y),{variável,n}]" calcula a n-ésima derivada parcial de f(x,y).

• O comando "D[f(x,y),x,y]" calcula a derivada parcial de f(x,y) primeiro em relação a y e depois em relação a x. O comando "D[f(x,y),y,x]" calcula a derivada parcial de f(x,y) primeiro em relação a x e depois em relação a y.

• O comando "Derivative" também pode ser usado para calcular a derivada parcial da função.

• O comando "Derivative[1,0][f][a,b]" calcula a derivada parcial de f em relação a x e apresenta o resultado trocando x por a, e y por b.

• O comando "Derivative[0,1][f][a,b]" calcula a derivada parcial de f em relação a y e apresenta o resultado trocando x por a, e y por b.

• O comando "Derivative[n,m][f][a,b]" calcula a n-ésima derivada parcial da f em relação a x e depois a m-ésima derivada parcial de f em relação a y e apresenta o resultado trocando x por a, e y por b.

Veja alguns exemplos a seguir:

Exemplo 4.8

Calcular as derivadas parciais da função f(x,y) = ln(3x³y)sen(x3y³) em relação a x e y.

Resolução

Utilizamos o comando "D" para calcular a derivada parcial. Podemos também derivar expressões que possuem variáveis independentes entre si. Assim sendo, assumimos que em "D[Log[3x³+y]+Sin[x+3y³],x]", y é independente de x, isto é, a derivada parcial de f(x,y) em relação a x é obtida utilizando o seguinte comando:

In[ ]:= D[Log[3 x^3+y]+Sin[x+3 y^3],x]
Out[ ]=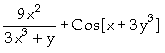

Analogamente, a derivada da f(x,y) em relação a y é obtida por

In[ ]:= D[Log[3 x^3+y]+Sin[x+3 y^3],y]
Out[ ]=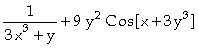

Observe que se y for dependente de x, podemos utilizar a forma funcional explícita y[x] e damos o seguinte comando:

In[ ]:= D[Log[3 x^3+y[x]]+Sin[x+3 y[x]^3],x]
Out[ ]=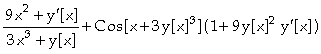

 Assim, concluímos que

• ;
• .

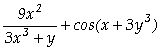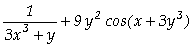Exemplo 4.9

Seja f(x,y) = (x³ y³)^3/5. Calcular

a) ;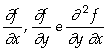
b) ;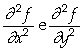

Resolução

Utilizamos os seguintes comandos:

In[ ]:= Clear[f]
        f[x,y]:=(x^3+y^3)^(3/5)

a) In[ ]:= D[f[x,y],x]
     Out[ ]=

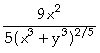
      In[ ]:= D[f[x,y],y]
       Out[ ]=

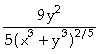
        In[ ]:= D[f[x,y],y,x]
        Out[ ]=

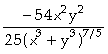
Assim, concluímos que

• ;
• ;
• .

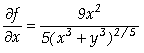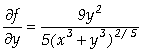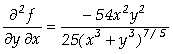 b)  In[ ]:= Clear[f]
             f[x,y]:=(x^3+y^3)^(3/5)

        In[ ]:= D[f[x,y],{x,2}]
        Out[ ]=

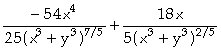
        In[ ]:= Together[%]
        Out[ ]=

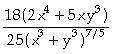
        In[ ]:= Together[D[f[x,y],{y,2}]]
        Out[ ]=

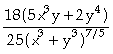
 Assim, concluímos que

•  = ;

• = .

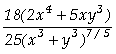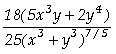Exemplo 4.10

Seja f(x,y) = log(x²y²) cos(xy). Calcular as seguintes derivadas parciais:

a) , , e ;
b) e ;
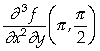c) e .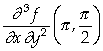

Resolução

Utilizamos o comando "Derivative" para calcular as derivadas parciais desejadas. Em alguns casos achamos o mesmo resultado aplicando o comando "D". Inicialmente, definimos a função f(x,y).

In[ ]:= Clear[f]
        f[x_,y_]:= Log[x^2+y^2] Cos[x+y]

a) In[ ]:= Derivative[1,0][f][x,y]
Out[ ]=

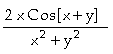
ou

In[ ]:= D[f[x,y],x]
Out[ ]=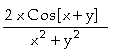

In[ ]:= Derivative[0,1][f][x,y]
Out[ ]=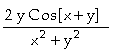

ou

In[ ]:= D[f[x,y],y]
Out[ ]=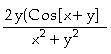

In[ ]:= Derivative[1,1][f][x,y]

Out[ ]=

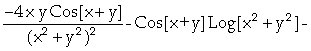
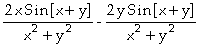
ou

In[ ]:= D[f[x,y],x,y]

Out[ ]= -

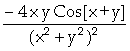
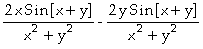
In[ ]:= Derivative[1,1][f][y,x]

Out[ ]=

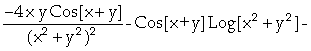
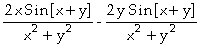
ou

In[ ]:= D[f[x,y],y,x]

Out[ ]= -

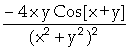
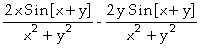
Assim, concluímos que

• ;
• ;
• ;

• .

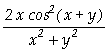
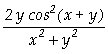
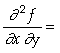
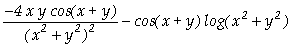
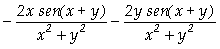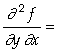
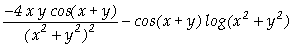
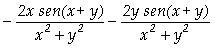b) In[ ]:= Derivative[2,0][f][x,y]

      Out[ ]=

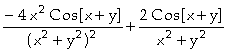
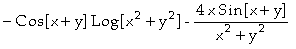
In[ ]:= [Derivative[0,2][f][x,y]]

Out[ ]=

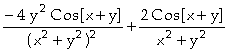
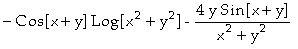
Assim, concluímos que

• ;

• .

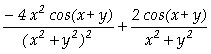
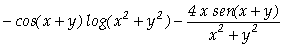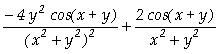
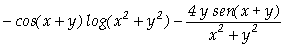c)  In[ ]:= Derivative[2,1][f][Pi,Pi/2]
     Out[ ]=

      In[ ]:= N[%]
      Out[ ]= -2.86925

       In[ ]:= Derivative[1,2][f][Pi,Pi/2]
       Out[ ]=

        In[ ]:= N[%]
        Out[ ]= - 2.67472

 Assim, concluímos que

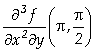• = - 2.86925;
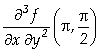• = - 2.67472.

4.4 Cálculo integral

Iniciamos esta seção com a computação de integrais definidas e indefinidas. Apresentamos também exemplos de cálculo de integrais duplas e triplas. Vamos ver os comandos que serão utilizados para estes cálculos:

• O comando "Integrate[f[x],x]" calcula a integral indefinida .

• O comando "Integrate[f[x],{x,x1,x2}]" calcula a integral definida .

•  O comando "Integrate[f[x,y],{x,x1,x2},{y,y1,y2}]" calcula a integral dupla definida .

•  O comando "Integrate[f[x,y,z],{x,x1,x2},{y,y1,y2}],{z,z1,z2}]" calcula a integral tripla definida .

Quando "Integrate" não consegue produzir o resultado exato da expressão numa forma adequada, usamos "NIntegrate"; ou, simplesmente, utilizamos "N[%]" para achar o valor exato da expressão anterior. "NIntegrate" também é usado nos cálculos das integrais, onde "Integrate" não consegue calcular o valor da integral.

Exemplo 4.11

Calcular as seguintes integrais:

a) ;
b) .

Resolução

Utilizamos os seguintes comandos para resolver as integrais:

a) In[ ]:= Integrate[x^3+5 x^2+3 x- 5,x]
     Out[ ]=

b) In[ ]:= Integrate[Log[x]/x^2,x]

      Out[ ]=

Assim, concluímos que

•  = ;

• = .

Exemplo 4.12

 a) ;
b) ;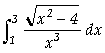
c) .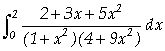

Resolução

As integrais são resolvidas usando os seguintes comandos:

a)  In[ ]:= Integrate[Cos[x],{x,0,Pi}]
     Out[ ]= 0

b) In[ ]:= Integrate[(Sqrt[x^2+4])/x^3,{x,1,3}]
     Out[ ]=

     In[ ]:= N[%]
     Out[ ]= 1.12235

c) In[ ]:= Clear[f]
            f[x_]:=(2+3 x+5 x^2)/((1+x^2)(4+9 x^2))
            NIntegrate[f[x],{x,0,2}]
     Out[ ]= 0.788964

Resolvemos a mesma integral utilizando o processo de frações parciais:

In[ ]:= Apart[f[x]]
Out[ ]=

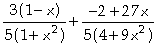
In[ ]:= Integrate[%,{x,0,2}]
Out[ ]=

O valor numérico da integral calculada acima é obtido utilizando o comando "N[%]"

In[ ]:= N[%]
Out[ ]= 0.788964

Assim, concluímos que

• = 0;
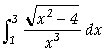• = 1,12235;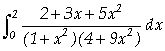
• = 0,788964.

Exemplo 4.13

Calcular as seguintes integrais duplas:

a) ;

b) ;

c) .

Resolução

Para resolver integrais duplas sabemos que

Partindo desta observação, calculamos as integrais usando os seguintes comandos:

a) In[ ]:= Integrate[y Cos[x]- x Cos[y],{x,0,Pi/2},y,0,Pi}]
     Out[ ]= .

In[ ]:= N[%]
Out[ ]= 4.9348

b) In[ ]:= Integrate[x^2 y,{y,0,3},{x,1- 2 y,y^2}]
     Out[ ]=

c) In[ ]:= NIntegrate[Cos[Exp[x y]],{x,0,1},{y,0,1}]
     Out[ ]= 0.245001

Assim, concluímos que

• =;
• =;
• = 0,245001.

Exemplo 4.14

Calcular as seguintes integrais triplas:

a) ;

b) ;

Resolução

Para resolver integrais duplas sabemos que

Partindo desta observação, calculamos as integrais triplas usando os seguintes comandos:

a) In[ ]:= Integrate[x y z,{x,1,2},{y,0,1},{z,1,3}]
     Out[ ]= 3

b) In[ ]:= Integrate[y Exp[z],{y,1,2},{x,0,y^2}, {z,0,Log[x]}]
      Out[ ]=

Assim, concluímos que

• = 3;
• = .

Observação

• No cálculo de integrais duplas e triplas deve-se cuidar na colocação dos limites das integrais nos comandos, isto é, quando uma variável está dependendo de outra, primeiro deve-se colocar os limites independentes e depois as variáveis dependentes. Veja a seguir os comandos: