5.1 Introdução

Neste capítulo apresentaremos cálculos de comprimento de arco e a área de região plana limitada utilizando coordenadas cartesianas, paramétricas e polares. Calcularemos a área de região plana limitada em coordenadas cartesianas e polares, aplicando o conceito de integral dupla. Área de superfície e volume do sólido de revolução também foram estudados. Também calcularemos o volume de um sólido, utilizando coordenadas polares e cartesianas em integração dupla. Utilizando a integração tripla também calcularemos o volume de um sólido em coordenadas cartesianas, cilíndricas e esféricas.

5.2 Comprimento de arco

Nesta seção apresentamos comprimento de arco de curva plana limitada em certo intervalo. Fazemos estes cálculos em três formas diferentes: primeiro em coordenadas cartesianas; depois em equações representadas parametricamente; finalmente, utilizando coordenadas polares.

5.2.1 Coordenadas cartesianas

Seja y = f(x) uma função contínua num intervalo [a,b]. O pedaço de curva do ponto A(a,f(a)) ao ponto B(b,f(b)) é chamado arco.

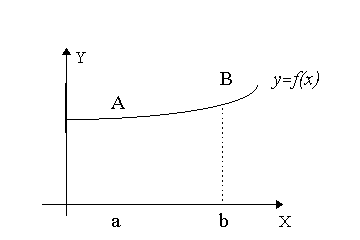
 O comprimento de arco da curva da função y = f(x) de A(a,f(a)) até B(b,f(b)) é dado por

A fórmula para o cálculo de comprimento de arco da função descrita em coordenadas cartesianas no Mathematica é dada por "Integrate[ Sqrt[1+[D[f[x],x]^2],{x,a,b}]", isto é,

Para calcular o comprimento de arco de uma curva, no Mathematica, inicialmente calculamos o valor da primeira derivada da função, através do comando "D". A seguir, utilizamos este resultado para calcular a integral que fornece o comprimento do arco, através do comando "Integrate".

Veremos agora, alguns exemplos de como encontrar o comprimento do arco de curvas representadas na forma cartesiana, através dos comandos do Mathematica.

Exemplo 5.1

Calcular o comprimento de arco das seguintes curvas no intervalo dado:

a) y = , 0 £ x £ 3;
b) x = 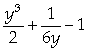, 1 £ y £ 3.

Resolução

Para calcular o comprimento de arco das curvas dadas, inicialmente traçamos os gráficos das curvas e depois calculamos o comprimento utilizando a fórmula dada inicialmente.

a) In[ ]:= Plot[((2+x^2)^(3/2))/3,{x,0,3}]

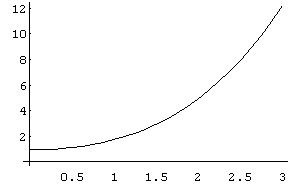
 Out[ ]= -Graphics-

In[ ]:= D[((2+x^2)^(3/2))/3,x]
Out[ ]= x Sqrt[2+x²]

In[ ]:= Integrate[Sqrt[1+(%)^2],{x,0,3}]
Out[ ]= 12

Logo, concluímos que o comprimento da curva é 12 u.c..

b) Veja os comandos a seguir:

In[ ]:= Plot[(1/2) y^3+1/(6 y)- 1,{y,1,3}, AxesLabel -> {"y","g(y)"}]

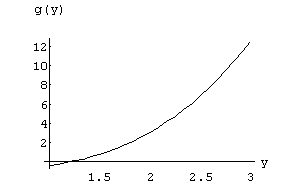
Out[ ]= -Graphics-

In[ ]:= D[(1/2) y^3+1/(6 y)-1,y]
Out[ ]=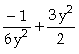

In[ ]:= Integrate[Sqrt[1+(%)^2],{y,1,3}]

Out[ ]=

In[ ]:= N[%]
Out[ ]= 13.1111

Logo, concluímos que o comprimento da curva é 13,1111 u.c..

5.2.2 Equações paramétricas

A fórmula para o cálculo de comprimento de arco é dada pela integral

onde x=x(t) e y=y(t), t Î [t_o,t₁] é a equação da curva dada na forma paramétrica.

 A fórmula para o cálculo de comprimento de arco no Mathematica é dada por "Integrate[Sqrt[[D[x[t],t]]^2+[D[y[t],t]]^2], {t,t0,t1}]", isto é,

A seguir damos exemplos de cálculo de comprimento de arco de uma curva dada em equações paramétricas.

Exemplo 5.2

Calcular o comprimento do arco das seguintes curvas dadas em equações paramétricas:

a) x(t) = t³, y(t) = t², t Î [1,3];
b) x(t) = 2 cos t - 2 t sen t, y(t) = 2 sen t - 2 t cos t, 0 £ t £ p /2.

Resolução

Para resolver estes exemplos, inicialmente traçamos os gráficos das curvas utilizando o comando "ParametricPlot". Depois aplicamos a fórmula dada acima com passos necessários para o cálculo de comprimento de arco das curvas, utilizando os comandos "D" e "Integrate".

a) In[ ]:= ParametricPlot[{t^3,t^2},{t,1,3}]

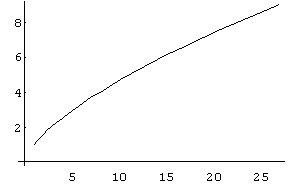
Out[ ]= -Graphics-

In[ ]:= D[{t^3,t^2},t]
Out[ ]= {3 t³,2 t}

In[ ]:= Integrate[Sqrt[(3 t^2)^2+(2 t)^2], {t,1,3}]
Out[ ]=

In[ ]:= N[%]
Out[ ]= 27.2885

Assim, concluímos que o comprimento de arco da curva dada é 27,2885 u.c..

b) In[ ]:= ParametricPlot[{2 Cos[t]- 2 t Sin[t],2 Sin[t]- 2 t Cos[t]}, {t,0,Pi/2}]

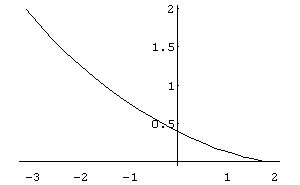
Out[ ]= -Graphics-

In[ ]:= D[{2 Cos[t]+2 t Sin[t],2 Sin[t]- 2 t Cos[t]},t]
Out[ ]= {2 t Cos[t], 2 t Sin[t]}

In[ ]:= Integrate[Sqrt[(2 t Cos[t])^2+(2 t Sin[t])^2], {t,0,Pi/2}]
Out[ ]=

In[ ]:= N[%]
Out[ ]= 2.4674

Assim, concluímos que o comprimento de arco da curva dada é 2,4674 u.c..

5.2.3 Coordenadas polares

Seja uma curva C dada na forma r = f(q). O comprimento de arco dessa curva desde q = q₁ até q = q₂ é dado pela integral

A fórmula para o cálculo de comprimento de arco em Mathematica é dada por "Integrate[Sqrt[[D[f[theta],theta]]^2 + [f[theta]^2]], {theta, theta1, theta2}]", isto é,

A seguir damos exemplos de cálculo do comprimento de arco das curvas escritas em coordenadas polares.

Exemplo 5.3

Calcular o comprimento de arco das seguintes curvas dadas em coordenadas polares:

a) r = 1 + cos q , 0 £ q £ 2p ;
b) r = q /4, 0 £ q £ 2p .

Resolução

Para resolver estes exemplos, traçamos inicialmente os gráficos das curvas utilizando o comando "PolarPlot". Para aplicar este comando, necessitamos do pacote "Graphics", o que fizemos carregando o pacote desejado utilizando primeiro o comando

In[ ]:= Needs["Graphics`Graphics`"]

Depois aplicamos a fórmula dada acima, com os passos necessários para o cálculo de comprimento de arco das curvas dadas.

a) In[ ]:= PolarPlot[1+Cos[theta],{theta,0,2 Pi}]

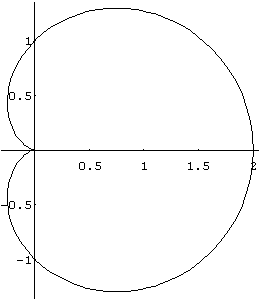
Out[ ]= -Graphics-

In[ ]:= D[1+Cos[theta],theta]
Out[ ]= -Sin[theta]

In[ ]:= Integrate[Sqrt[- Sin[theta])^2 + (1+Cos[theta])^2],{theta,0,Pi}]
Out[ ]= -4

In[ ]:= Abs[%]
Out[ ]= 4

Logo, concluímos que o comprimento do arco acima é 2.4 = 8 u.c..

Observação

• Observe que no cálculo de integral utilizamos o intervalo de 0 a p , tendo em vista a simetria da figura em relação ao eixo x, e duplicamos o resultado após feito o cálculo.

 b) In[ ]:= PolarPlot[theta/4,{theta,0,2 Pi}]

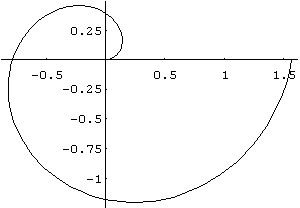
Out[ ]= -Graphics-

In[ ]:= D[theta/4,theta]
Out[ ]=

In[ ]:= Integrate[Sqrt[(theta/4)^2+(1/4)^2], {theta,0,2 Pi}]
Out[ ]=

In[ ]:= N[%]
Out[ ]= 5.31407

Logo, concluímos que o comprimento total da cardióide é 5,31407 p u.c..