5.3 Área de uma região plana

Nesta seção apresentamos o cálculo da área de uma região limitada. Fazemos estes cálculos em três formas diferentes: primeiro em coordenadas cartesianas; segundo em equações representadas parametricamente; finalmente, utilizando as coordenadas polares. Também utilizamos a integração dupla e tripla para fazer o cálculo de área de uma região plana.

5.3.1 Coordenadas cartesianas

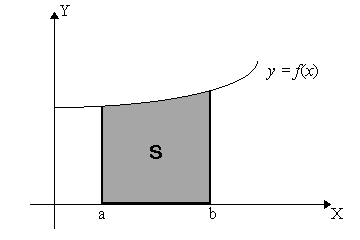
Seja y = f(x) uma função limitada pelas retas x = a, x = b e o eixo x, onde f é contínua em [a,b].

Neste, caso a área é dada por

 A fórmula para o cálculo de área no Mathemática é dada por "Integrate[f[x],{x,a,b}]", isto é,

Se o valor obtido for negativo utilize o comando "Abs" para calcular o valor absoluto.

A seguir damos exemplos de cálculo de área de regiões limitadas por curvas dadas em coordenadas cartesianas.

Exemplo 5.4

a) Encontrar a área limitada pela curva y = x² - 9 e o eixo x;

b) Encontrar a área da região limitada pela curva y = cos x e pelo eixo x de 0 até p .

Resolução

Para resolver estes exemplos, inicialmente traçamos os gráficos das curvas utilizando o comando "FilledPlot", o que representa a área solicitada. Para aplicar este comando necessitamos do pacote "FilledPlot", utilizando o seguinte comando:

In[ ]:= Needs["Graphics`FilledPlot`"]

Depois aplicaremos a fórmula de cálculo da área dada acima, com as passos necessários. Também utilizamos o comando "Solve" para achar os pontos de interseção das curvas com o eixo x.

a) In[ ]:= Solve[x^2- 9,x]
     Out[ ]= {{x -> 3}, {x -> - 3}}

Observemos que a curva dada intercepta o eixo x nos pontos -3 e 3. A seguir damos o gráfico da área desejada com o seguinte comando:

In[ ]:= FilledPlot[x^2- 9,{x,- 3,3}]

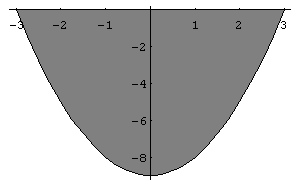
Out[ ]= -Graphics-

In[ ]:= Integrate[x^2- 9,{x,- 3,3}]
Out[ ]= - 36

In[ ]:= Abs[%]
Out[ ]= 36

Logo, concluímos que a área procurada é 36 u.a..

b) In[ ]:= FilledPlot[Cos[x],{x,0,Pi}]

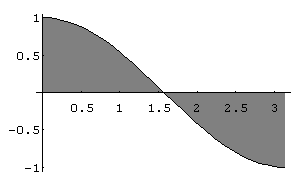
Out[ ]= -Graphics-

Pela simetria da figura, calculamos a área de 0 até p /2 e depois duplicamos o resultado. Veja os comandos a seguir:

In[ ]:= Integrate[Cos[x],{x,0,Pi/2}]
Out[ ]= 1

In[ ]:= Integrate[Cos[x],{x,Pi/2,Pi}]
Out[ ]= -1

In[ ]:= 2 Abs[%]
Out[ ]= 2.

Logo, concluímos que a área total é igual a 2 u.a..

A seguir apresentamos exemplos de cálculo de áreas delimitadas por curvas.

Exemplo 5.5

a) Encontrar a área limitada pela curva y = 5 - x² e a reta y = x + 3;
b) Encontrar a área limitada pela curva y = x³ - x e a reta y = 0;
c) Encontrar a área limitada pelas curvas dadas na forma implícita y² = 2x e x² = 2y.

Neste caso a área é calculada através da diferença entre a área sobre o gráfico da f e a área sobre o gráfico da g, ou seja:

Utilizando o software Mathematica o comando para o cálculo de área é dado por "Integrate[f[x]-g[x], {x,a,b}]", isto é,

 Resolução

 Para resolver estes exemplos, inicialmente traçamos os gráficos das curvas utilizando o comando "FilledPlot", para representar a área solicitada. Para aplicar este comando necessitamos do pacote "FilledPlot", que é carregado com o seguinte comando:

 In[ ]:= Needs["Graphics`FilledPlot`"]

Depois aplicamos a fórmula de cálculo de área, dada acima, com os passos necessários. Também utilizamos o comando "Solve" para achar os pontos de interseção das curvas. No exemplo c) também utilizaremos o comando "ImplicitPlot", carregando o pacote necessário.

a) In[ ]:= Solve[{y==5- x^2,y==x+3},x]
     Out[ ]= {{x -> - 2}, {x -> 1}}

Assim concluímos que as curvas dadas interceptam nos pontos x = - 2 e x = 1. A seguir utilizamos o comando "FilledPlot" para mostrar a área desejada:

In[ ]:= FilledPlot[{5- x^2,x+3},{x,- 2,1}]

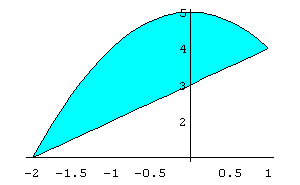
Out[ ]= -Graphics-

In[ ]:= Integrate[{5- x^2,x+3},{x,- 2,1}]
Out[ ]=

In[ ]:=N[12- 15/2]
Out[ ]= 4.5

Logo, a área da região é igual a 4,5 u.a..

b) In[ ]:= Solve[x^3- x==0,x]
Out[ ]= {{x -> 1},{x -> - 1},{x -> 0}}

As curvas interceptam-se nos pontos cujas abcissas são - 1, 0 e 1.

In[ ]:= FilledPlot[{x^3- x,0},{x,- 1,1}]

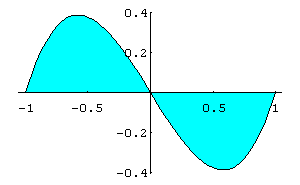
Out[ ]= -Graphics-

A área desejada é obtida através da soma das integrais que fornecem as áreas para cada um dos intervalos.

In[ ]:= Integrate[(x^3- x),{x,0,1}]
Out[ ]=

In[ ]:= Integrate[(x- x^3),{x,- 1,0}]
Out[ ]=

In[ ]:= 2 %
Out[ ]=

Logo, a área desejada é 0,5 u.a..

c) In[ ]:= Solve[{y^2==2 x,x^2==2 y},{x,y}]
    Out[ ]= {{x->2, y->2}, {x->2 (- 1)^4/3, y->2 (- 1)^2/3},{x->2 (- 1)^2/3, y->2 (- 1)^4/3},{x->0, y->0}}

No plano cartesiano as curvas se interceptam nos pontos (0,0) e (2,2). A seguir construímos o gráfico das curvas utilizando o comando "ImplicitPlot".

In[ ]:= Needs["Graphics`ImplicitPlot`"]

In[ ]:= ImplicitPlot[{y^2==2 x,x^2==2 y},{x,- 2,2.5}]

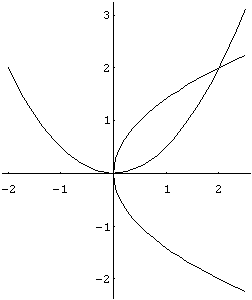
Out[ ]= -Graphics-

In[ ]:= FilledPlot[{Sqrt[2 x],x^2/2},{x,0,2}]

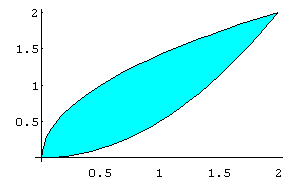
Out[ ]= -Graphics-

In[ ]:= Integrate[{Sqrt[2 x],x^2/2},{x,0,2}]
Out[ ]=

In[ ]:= 8/3- 4/3
Out[ ]=

Logo, concluímos que a área da região é igual a u.a..

5.3.2 Equações paramétricas

Seja S uma região limitada pela função f, pelas retas x = a, x = b e o eixo x, onde f é contínua em [a,b]. A fórmula para o cálculo de área de uma região representada por equações paramétricas é dada pela integral

onde x=x(t) e y=y(t), t Î [t_o,t₁], é a equação da função y = f(x) dada na forma paramétrica.

A fórmula para o cálculo de área em coordenadas paramétricas, utilizando o software Mathematica, é dada por "Integrate[y[x]D[x[t],t],{x,t0,t1}]", isto é,

A seguir damos exemplos de cálculo de área de regiões limitadas por curvas escritas por equações paramétricas.

Exemplo 5.6

a) Encontrar a área da região limitada pela elipse ;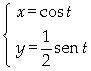
 b) Calcular a área delimitada pela hipociclóide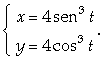

Resolução

a) Primeiramente construímos a figura das equações dadas utilizando o comando "ParametricPlot". Veja o comando utilizado a seguir:

In[ ]:= ParametricPlot[{Cos[t],1/2 Sin[t]},{t,0,2 Pi}]

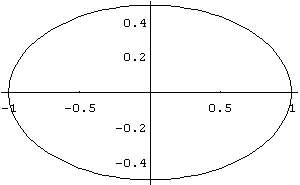
Out[ ]= -Graphics-

Pela simetria da figura acima em relação aos eixos, é suficiente calcular a área da região somente no primeiro quadrante, isto é, de t variando de 0 a p /2, e posteriormente multiplicando o resultado por quatro.

In[ ]:= D[Cos[t],t]
Out[ ]= -Sin[t]

In[ ]:= Integrate[1/2 Sin[t] %,{t,0,Pi/2}]
Out[ ]= .

In[ ]:= Abs[%]
Out[ ]= .

Como este valor refere-se à área no primeiro quadrante, a área total é dada por 4.= u.a..

b) In[ ]:= ParametricPlot[{4 Sin[t]^3,4 Cos[t]^3}, {t,0,2 Pi}, AspectRatio->Automatic]

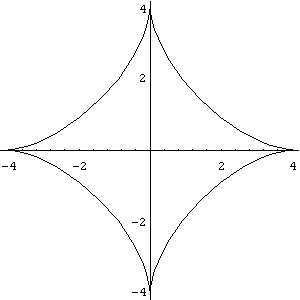
Out[ ]= -Graphics-

Pela simetria da figura, neste caso, também calcularemos a área limitada apenas no 1^o quadrante e depois multiplicaremos o resultado obtido por quatro.

In[ ]:= D[4 Sin[t]^3,t]
Out[ ]= 12 Cos[t] Sin[t]²

In[ ]:= Integrate[4 Cos[t]^3 %,{t,0,Pi/2}]
Out[ ]= .

In[ ]:= 4 %
Out[ ]= 6 Pi

Logo, a área desejada é 6p u.a..

Exemplo 5.7

Calcular a área limitada pelas curvas 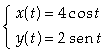e .

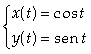Resolução

Utilizando o comando "ParametricPlot" construímos o gráfico das curvas:

In[ ]:= ParametricPlot[{{Cos[t],Sin[t]}, {4 Cos[t],2 Sin[t]}},{t,0,2 Pi}, AspectRatio->Automatic]

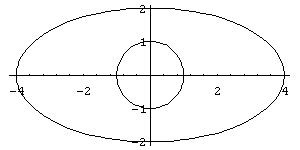
Out[ ]= -Graphics-

Pela simetria do gráfico em relação aos eixos, calculamos apenas a área da região que está no primeiro quadrante e, posteriormente, multiplicamos o resultado por quatro.

In[ ]:= D[{Cos[t],4 Cos[t]},t]
Out[ ]= {- Sin[t], - 4 Sin[t]}

In[ ]:= Integrate[{Sin[t] (- Sin[t]), 2 Sin[t] (- 4 Sin[t])},{t,Pi/2,0}]
Out[ ]=

In[ ]:= 4 Abs[Pi/4- 2 Pi]
Out[ ]= 7 Pi

Logo, a área desejada é 7p u.a..

5.3.3 Coordenadas polares

A fórmula para o cálculo da área da uma figura delimitada pelas retas q = q₁ e q = q₂ e pela curva r = f(q) é dada por

A fórmula para o cálculo de área em coordenadas polares utilizando o software Mathematica é dada por "1/2 Integrate[f[theta]^2, {theta, theta1, theta2}]", isto é,

A seguir damos exemplos de cálculo de área de regiões limitadas por curvas escritas na forma polar.

Exemplo 5.8

a) Calcular a área limitada pela curva r = cos 3q ;
b) Encontrar a área limitada pela curva r = 3 - 2 cos q ;
c) Encontrar a área interior da circunferência r = 3 sen q e exterior ao r = 1+ sen q .

Resolução

Para resolver estes exemplos, inicialmente traçamos os gráficos das curvas utilizando o comando "PolarPlot", para representar a área solicitada. Para aplicar este comando, necessitamos carregar o pacote desejado, utilizando primeiro o seguinte comando:

In[ ]:= Needs["Graphics`Graphics`"]

Depois aplicamos a fórmula de cálculo de área dada acima, com os passos necessários.

a) In[ ]= PolarPlot[Cos[3 theta],{theta,0,Pi}]

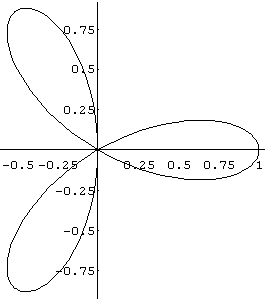
Out[ ]= -Graphics-

In[ ]:= Integrate[(Cos[3 theta])^2,{theta,0,Pi}]
Out[ ]=

A área total é dada por , ou seja, A = u.a..

b) In[ ]:= PolarPlot[3- 2 Cos[theta], {theta,0,2Pi}]

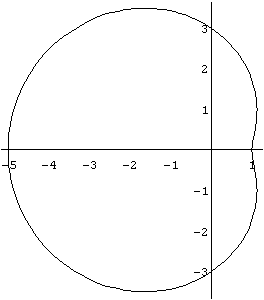
 Out[ ]= -Graphics-

Conforme a simetria do gráfico em relação ao eixo dos y, calculamos a integral da função de 0 a p , e posteriormente duplicamos o resultado.

In[ ]:= Integrate[(3- 2 Cos[theta])^2,{theta,0,Pi}]
Out[ ]= 11 Pi

Sendo assim, A = 2= 11p u.a..

c) In[ ]:= PolarPlot[{3 Sin[theta],1+Sin[theta]}, {theta,0,2 Pi}]

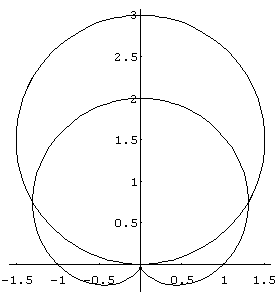
Out[ ]= -Graphics-

Aplicamos a seguir o comando "Solve" para achar os pontos de interseção destas curvas:

In[ ]:= Solve[3 Sin[theta]==1+Sin[theta],theta]
Out[ ]= {theta -> }

Neste caso, obtemos os pontos de intersecção das funções, que são q = - p /6 e q = p /6, onde utilizamos a simetria dada na figura, pois o comando "Solve" utilizado acima dá apenas um valor. Devido à simetria do gráfico em relação ao eixo x, calculamos a integral de 0 a p /6, sendo que neste caso, a área é dada pela subtração da área da cardióide da área do círculo.

In[ ]:= Integrate[(3 Sin[theta])^2 - (1+Sin[theta])^2,{theta,Pi/6,Pi/2}]
Out[ ]= Pi

Logo, concluímos que a área desejada é 2p = p u.a..

5.3.4 Área de uma região plana usando integral dupla

Nesta subseção apresentamos o cálculo de área usando integral dupla. Estes cálculos são feitos utilizando o sistema de coordenadas cartesianas e coordenadas polares.

5.3.4.1 Coordenadas cartesianas

A fórmula de cálculo de área de uma região plana limitada no sistema cartesiano utilizando integral dupla é dada por

onde R é a região plana limitada pela função y = f(x), x = a, x = b e o eixo dos x.

A fórmula para o cálculo de área utilizando o software Mathematica com integração dupla é dada por "Integrate[1,{x,a,b},{y,f[x1],f[x2]}]", isto é,

Veja a seguir alguns exemplos:

Exemplo 5.9

a) Calcular a área da figura limitada pela parábola y² = 2x e a reta y = x;
b) Calcular a área da figura limitada pelas curvas y = sen x, y = cos x e x = 0.

Resolução

a) Utilizamos o comando "Solve" para achar os pontos de interseção no eixo x:

In[ ]:= Solve[Sqrt[2 x]==x,x]
Out[ ]= {{x -> 0},{x -> 2}}

In[ ]:= Plot[{Sqrt[2 x],x},{x,0,2}]

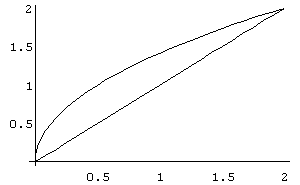
Out[ ]= -Graphics-

In[ ]:= Integrate[1,{x,0,2},{y,x,Sqrt[2 x]}]
Out[ ]=

Assim concluímos que a área da região desejada é u.a..

b) Neste caso podemos achar os pontos de interseção das curvas y= sen x e y= cos x simplificando a equação sen x = cos x, o que nos dá, x = . Traçando os gráficos das curvas y = sen x e y = cos x achamos a área a ser calculada. Veja o comando a seguir:

In[ ]:= Plot[{Sin[x],Cos[x]},{x,0,Pi/2}]

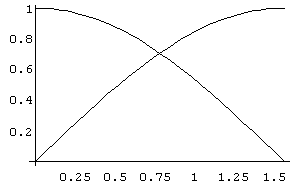
Out[ ]= -Graphics-

No gráfico acima não está bem clara a área a ser calculada. Então, utilizamos o comando "FilledPlot" para encontrar a região exata. Veja os comandos a seguir:

In[ ]:= Needs["Graphics`FilledPlot`"]

In[ ]:= FilledPlot[{Sin[x],Cos[x]},{x,0,Pi/4}]

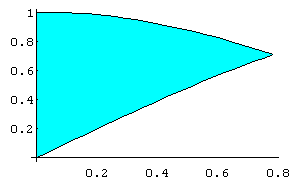
Out[ ]= -Graphics-

In[ ]:= Integrate[1,{x,0,Pi/4},{y,Sin[x],Cos[x]}]
Out[ ]= -1 + Sqrt[2]

Assim concluímos que a área da região desejada é u.a..

5.3.4.2 Coordenadas polares

A fórmula para o cálculo de área de uma figura plana descrita em coordenadas polares r = f(q ) é dada por

onde R é a região para o cálculo da área.

A fórmula para o cálculo de área utilizando o software Mathematica com integração dupla é dada por "Integrate[r,{theta,theta1,theta2},{r, f[theta1],f[theta2]}], isto é,

Veja a seguir alguns exemplos:

Exemplo 5.10

a) Encontre por integração dupla a área da região limitada por uma pétala da rosácea y = sen 2q ;
b) Encontre por integração dupla a área da região limitada pela cardióide r = 2(1 + cos q ).

Resolução

Para resolver estes exemplos necessitamos utilizar o comando "PolarPlot". Este comando está contido no pacote que carregamos dando o seguinte o comando:

In[ ]:= Needs["Graphics`Graphics`"]

a) Inicialmente construímos o gráfico da curva r = sen 2q utilizando o comando "PolarPlot":

In[ ]:= PolarPlot[Sin[2 theta],{theta,0,2 Pi}]

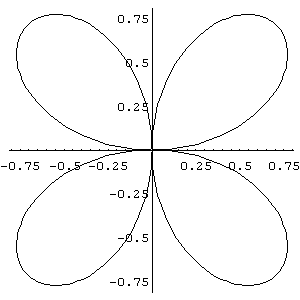
Out[ ]= -Graphics-

Analisando o gráfico acima vimos que ele apresenta quatro pétalas no intervalo de 0 a 2p . Se construirmos o mesmo gráfico no intervalo de 0 a p /2, acharemos a área desejada. Veja o comando a seguir:

In[ ]:= PolarPlot[Sin[2 theta],{theta,0,Pi/2}]

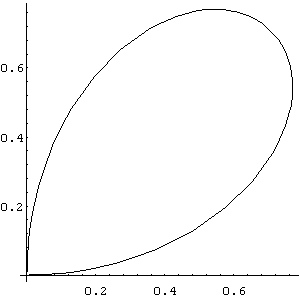
Out[ ]= -Graphics-

Aplicando o comando "Integrate" utilizando o conceito de integral dupla achamos a área da região solicitada. Veja o comando a seguir:

In[ ]:= Integrate[r,{theta,0,Pi/2},{r,0,Sin[2 theta]}]
Out[ ]=

Assim concluímos que a área da região desejada é u.a..

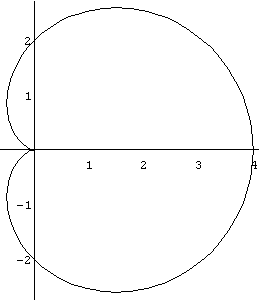
b) Inicialmente construímos o gráfico da curva r = 2(1+ cos q ) utilizando o comando "PolarPlot":

In[ ]:= PolarPlot[2(1+Cos[theta]),{theta,0,2 Pi}]

Out[ ]= -Graphics-

Pela simetria do gráfico em relação ao eixo x, calculamos a área da região onde q varia de 0 a p e duplicaremos o resultado. Veja o comando a seguir:

In[ ]:= Integrate[r,{theta,0,Pi},{r,0,2(1+Cos[theta])}]
Out[ ]= 3 Pi

Assim concluímos que a área desejada é 2´ 3p , isto é, 6p u.a..

5.3.5 Área de uma superfície de revolução

Um sólido de revolução é obtido fazendo-se uma região plana girar em torno de uma reta no plano, sendo que a reta ao redor da qual a região gira é chamada eixo de revolução. A seguir damos fórmulas de cálculo de volumes e áreas de superfície, dependendo do eixo da rotação. Nesta seção damos o volume e a área da superfície do sólido de revolução obtido pela rotação de uma curva em torno de um eixo fixo.

A área da uma superfície de revolução obtida por revolução da região limitada pelo gráfico de y = f(x), x = a, x = b, e o eixo x em torno do eixo x é dada por

e em torno do eixo y é dada por

A fórmula para o cálculo de área de uma superfície de revolução em torno do eixo x utilizando Mathematica é dada por "Pi Integrate[f[x]Sqrt [1 +[D[f[x], x]]^2], {x,a,b}]", isto é,

e em torno do eixo y é dada por "Pi Integrate[x Sqrt[1+[D[f[x],x]]^2], {x,a,b}]", isto é,

A área do sólido de revolução obtido por revolução da região limitada pelo gráfico de x = g(y), y = c, y = d, e o eixo y em torno do eixo y é dada por

e em torno do eixo x é dada por

A fórmula para o cálculo de área de uma superfície de revolução em torno do eixo y utilizando Mathematica é dada por "Pi Integrate[g[y] Sqrt[1+[D[g[y],y]]^2],{y,c,d}]", isto é,

e em torno do eixo x é dada por "Pi Integrate[y Sqrt[1+[D[g[y],y]]^2], {y,c,d}]", isto é,

A seguir damos exemplos de cálculo de área de uma superfície de revolução:

Exemplo 5.11

a) Encontrar a área da superfície gerada pela rotação do arco da curva com 1 £ x £ 12
      i) em torno do eixo x;
      ii) em torno do eixo y.
b) Encontrar a área da superfície gerada pela rotação do arco da curva y = x²/3, com 0 £ x £ 2
     i) em torno do eixo x;
     ii) em torno do eixo y.

Resolução

Para gerar o sólido de revolução carregamos o pacote desejado, utilizando o seguinte comando:

In[ ]:= Needs["Graphics`SurfaceOfRevolution`"]

A seguir resolvemos o exemplo dado construindo o gráfico da função e da superfície gerado após revolução em torno do eixo x, e efetuamos os cálculos necessários.

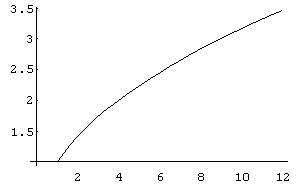
a) In[ ]:= Plot[Sqrt[x],{x,1,12}]

Out[ ]= -Graphics-

A seguir faremos este exemplo em duas partes, uma em torno do eixo x e outra em torno do eixo y:

a) i) Rotação em torno do eixo x

Inicialmente apresentamos o gráfico tridimensional utilizando os comandos "SurfaceOfRevolution" e "ParametricPlot3D". Veja a seguir que os dois comandos apresentam o mesmo gráfico:

In[ ]:= SurfaceOfRevolution[Sqrt[x],{x,1,12}, Axis->{1,0,0}]
ou
In[ ]:= Clear[f]
        f[x_]:= Sqrt[x]
        ParametricPlot3D[{x,f[x] Cos[t],f[x] Sin[t]},{x,1,12},{t,0,2 Pi}]

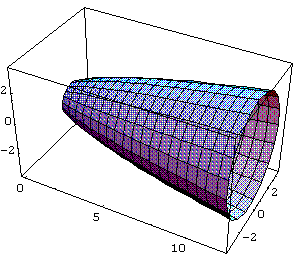
Out[ ]= -Graphics3D-

In[ ]:= D[Sqrt[x],x]
Out[ ]=

In[ ]:= 2 Pi Integrate[Sqrt[x] Sqrt[1+(%)^2],{x,1,12}]
Out[ ]=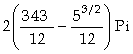

In[ ]:= N[%]
Out[ ]= 173.74

Logo, a área da superfície gerada pela rotação é dada por 173,74 u.a..

a) ii) Rotação em torno do eixo y

Inicialmente apresentamos o gráfico tridimensional utilizando os comandos "SurfaceOfRevolution" e "ParametricPlot3D". Veja a seguir que os dois comandos apresentam o mesmo gráfico:

In[ ]:= SurfaceOfRevolution[Sqrt[x],{x,1,12},Axis->{0,0,1}]

ou

In[ ]:= ParametricPlot3D[{x Cos[t],x Sin[t],Sqrt[x]},{x,1,12},{t,0,2 Pi}]

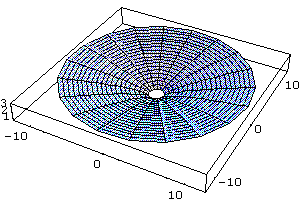
Out[ ]= -Graphics3D-

In[ ]:= D[Sqrt[x],x]
Out[ ]=

In[ ]:= 2 Pi Integrate[x Sqrt[1+(%)^2],{x,1,12}]
Out[ ]=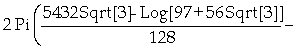

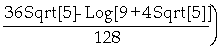
In[ ]:= N[%]
Out[ ]= 457.77

Logo, concluímos que a área desejada é 457,77 u.a..

b) Inicialmente construímos o gráfico da função utilizando o comando "Plot":

In[ ]:= Plot[x^2/3,{x,-2,2}]

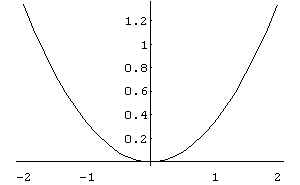
Out[ ]= -Graphics-

A seguir faremos este exemplo em duas partes, uma em torno do eixo x e outra em torno do eixo y:

b) i) Rotação em torno do eixo x

Apresentamos o gráfico tridimensional utilizando os comandos "SurfaceOfRevolution" e "ParametricPlot3D". Veja a seguir que os dois comandos apresentam o mesmo gráfico:

In[ ]:= SurfaceOfRevolution[x^2/3,{x,- 2,2}, Axis->{1,0,0}]
ou
In[ ]:= Clear[f]
        f[x_]:= x^2/3
        ParametricPlot3D[{x,f[x] Cos[t],f[x] Sin[t]}, {x,- 2,2},{t,0,2 Pi}]

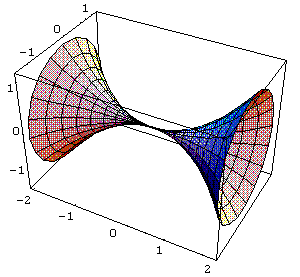
Out[ ]= -Graphics3D-

In[ ]:= D[x^2/3,x]
Out[ ]=

 In[ ]:= 2 Pi Integrate[x^2/3 Sqrt[1+(%)^2],{x,- 2,2}]
Out[ ]=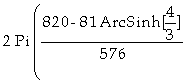

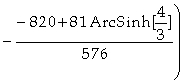
In[ ]:= N[%]
Out[ ]= 15.9482

Logo, a área da superfície gerada pela rotação é dada por 15,9482 u.a..

b) ii) Rotação em torno do eixo y

Apresentamos o gráfico tridimensional utilizando os comandos "SurfaceOfRevolution" e "ParametricPlot3D". Veja a seguir que os dois comandos apresentam o mesmo gráfico:

In[ ]:= SurfaceOfRevolution[x^2/3,{x,-2,2}, Axis->{0,0,1}]
ou
In[ ]:= ParametricPlot3D[{x Cos[t],x Sin[t],x^2/3},{x,-2,2},{t,0,2 Pi}]

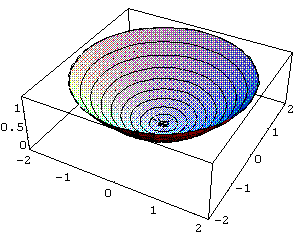
Out[ ]= -Graphics3D-

In[ ]:= D[x^2/3,x]
Out[ ]=

In[ ]:= 2 Pi Integrate[x Sqrt[1+(%)^2],{x,0,2}]
Out[ ]=

Logo, a área da superfície gerada pela rotação é dada por u.a..

Observações

• No exemplo acima consideramos o intervalo de cálculo de 0 a 2 em vez de -2 a 2. Isto se deve ao fato de que o gráfico é simétrico em relação ao eixo y. Veja a seguir a construção do mesmo gráfico (superfície de revolução), onde x varia de 0 a 2:

In[ ]:= ParametricPlot3D[{x Cos[t],x Sin[t],x^2/3},{x,0,2},{t,0,2 Pi}]

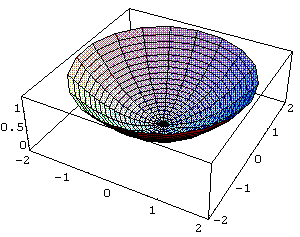
 Out[ ]= -Graphics3D-

 Os comandos utilizados tem suas explicações a seguir:

•  A utilização do comando "SurfaceOfRevolution" tem as seguintes opções básicas:
• O primeiro argumento representa a função y = f(x);
• O segundo argumento representa a variação de x;

• O terceiro argumento (opcional) indica o eixo de rotação, caso não o coloquemos, o programa traça o sólido em torno do eixo y, isto é, Axis->{0,0,1}. Em plano é a rotação em torno do eixo y, mas em três dimensões é em torno do eixo z;

• A utilização do comando "ParametricPlot3D" já explicamos no capítulo anterior.