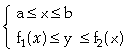
5.4 Volume de um sólido

Nesta seção damos o volume de um sólido em várias formas, utilizando sistema cartesiano, coordenadas polares, coordenadas cilíndricas, coordenadas esféricas, volume de um sólido de revolução, etc..

5.4.1 Coordenadas cartesianas

Nesta subseção apresentamos volume de um sólido cujas equações são dadas em coordenadas cartesianas. Estes cálculos são feitos em duas partes. Primeira, utilizando a integração dupla e a segunda, utilizando a integração tripla.

5.4.1.1 A integração dupla

Seja R uma região do plano xy representada por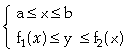

Seja g(x,y) uma função contínua de duas variáveis tal que g(x,y) ³ 0 para todo (x,y) na região R. O volume V do sólido compreendido entre o gráfico de z = g(x,y) e acima de R é dado por

ou

Utilizando os comandos do Mathematica a fórmula dada acima é representada por "Integrate[1,{x,a,b},{y,f1(x),f2(x)}]", isto é,

Veja a seguir alguns exemplos para o cálculo de volume em coordenadas cartesianas utilizando a integração dupla:

Exemplo 5.12

a) Encontrar o volume do sólido limitado pela superfície g(x,y) = e os planos x = 4 e y = 3 e os três planos coordenados; 

b) Encontrar o volume do espaço limitado pelas superfícies x = 0, y = 0, z = 0 e x + y + z = 1.

Resolução

a) É dado que g(x,y) = e as variações de x e y são 0 £ x £ 4 e 0 £ y £ 3, respectivamente. Colocando estes valores na integral que dá o volume, obtemos

Utilizando o comando "Integrate", obtemos

 In[ ]:= Integrate[2- 1/3 x^2 + 1/6 y^2,{x,0,4},{y,0,3}]
Out[ ]=

Logo, concluímos que o volume do espaço desejado é dado por V = u.v..

b) É dado que x + y + z = 1, daí achamos o valor da função g(x,y), isto é, z = g(x,y) = 1 - x - y. Como é dado que z = 0, daí concluímos que x + y = 1, isto é, y = 1 - x. Quando y = 0 em x + y = 1 achamos o valor máximo de x, isto é, x = 1. Resumindo temos as seguintes variações:

Substituindo estes valores na integral que dá o volume obtemos

Damos o seguinte comando para calcular o valor da integral:

In[ ]:= Integrate[1- x- y,{x,0,1},{y,0,1- x}]
Out[ ]=

Logo, concluímos que o volume desejado é dado por V = u.v..

5.4.1.2 Cálculo de volume utilizando a integração tripla

 Seja T uma região qualquer no plano xyz. Projetamos a região T sobre o plano xy e obtemos a região plana R limitada por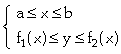

Se a região T é limitada por z₁ = g₁(x,y) e z₂ = g₂(x,y), então o volume da região T é dado por

ou

Utilizando os comandos do Mathematica a fórmula dada acima é representada por "Integrate[1,{x,a,b},{y,f1(x),f2(x)}, {z,g1(x),g2(x)}]", isto é,

Veja a seguir alguns exemplos para o cálculo de volume em coordenadas cartesianas utilizando integral tripla.

 Exemplo 5.13

a) Encontrar o volume do sólido limitado superiormente por z = x + 2y + 4, inferiormente por z = - x - 2y + 2 e lateralmente pela superfície definida pelo contorno da região D, limitada pelas curvas y = x² - 1 e y = 2x² - 2;

b) Encontrar o volume do sólido limitado abaixo pelo plano z = 0, lateralmente pelo cilindro elíptico x² + y² = 1 e acima pelo plano z = x + y + 1.

Resolução

a) Inicialmente damos o comando "Solve" para achar os limites de x:

In[ ]:= Solve[x^2- 1==2 x^2- 2,x]
Out[ ]= {{x -> 1}, {x -> - 1}}

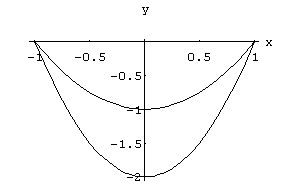
Assim achamos os valores de x que variam de -1 a 1. A variação de y já foi dada, isto é, x² -1 £ y £ 2 x² - 2. Veja no gráfico abaixo estas duas curvas:

In[ ]:= Plot[{x^2-1,2 x^2-2}, {x,-1,1}, AxesLabel->{"x","y"}]

Out[ ]= -Graphics-

Os valores de z já estão dados no próprio enunciado do exemplo, isto é, z varia de - x - 2 y + 2 a x + 2 y + 1. Resumindo, temos as seguintes variações de x, y e z no sólido T:

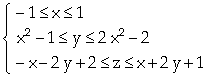
O volume do sólido é dada pela integral

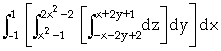Utilizando o comando "Integrate" temos o resultado desejado:

In[ ]:= Integrate[1,{x,- 1,1},{y,x^2- 1,2 x^2- 2}, {z,- x- 2 y+2, x+2 y+1}]
Out[ ]=

Logo, concluímos que o volume desejado é u.v..

b) Inicialmente damos o comando "Solve" para achar as variações de x, onde consideramos y = 0:

In[ ]:= Solve[{x^2+y^2==1,y==0},x]
Out[ ]= {{x -> 1}, {x -> - 1}}

Assim achamos os valores de x, que variam de -1 a 1.

Veja a seguir o gráfico da equação x² + y² = 1, onde utilizamos o comando "ImplicitPlot":

In[ ]:= Needs["Graphics`ImplicitPlot`"]
       ImplicitPlot[x^2+y^2==1,{x,- 1,1}]

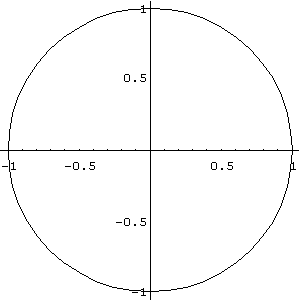
Out[ ]= -Graphics-

As variações de y são obtidas novamente utilizando o comando "Solve":

In[ ]:= Solve[x^2+y^2==1,y]
Out[ ]= {{y->Sqrt[1- x²]},{y->- Sqrt[1- x²]}}

Assim, achamos as variações de y, isto é . As variações de z já são dadas, isto é, 0 £ z £ x+y+1.

Resumindo, temos as seguintes variações de x, y e z no sólido T:

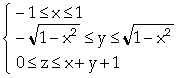
O volume do sólido é dada pela integral

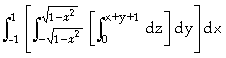Utilizando o comando "Integrate" temos o resultado desejado:

In[ ]:= Integrate[1,{x,- 1,1},{y,- Sqrt[1- x^2], Sqrt[1- x^2]},{z,0,x+y+1}]
Out[ ]= Pi

Logo, concluímos que o volume do sólido é dado por V = p u.v..

5.4.2 Coordenadas polares e cilíndricas

Nesta subseção apresentamos o cálculo de volume de um sólido cujas equações são dadas em coordenadas polares ou cilíndricas.

5.4.2.1 Coordenadas polares

A fórmula para o cálculo de volume de um espaço representado em cordenadas polares é dada por

 onde 0 £ r £ a, 0 £ q £ 2p .

A fórmula acima é a mesma utilizada no cálculo de volume em coordenadas cartesianas por integração dupla, com x = r cos q , y = r sen q e dx dy = r dr dq .

Utilizando os comandos do Mathematica a fórmula dada acima é representada por "Integrate[g(r,theta), {r,0,a},{theta,0,2 Pi}]", isto é,

A seguir apresentamos alguns exemplos de cálculo de volume em coordenadas polares utilizando integração dupla.

 Exemplo 5.14

a) Utilizar as coordenadas polares para encontrar o volume do sólido limitado pela esfera x² + y² + z² = a²;

b) Utilizar as coordenadas polares para encontrar o volume do sólido limitado pelas superfícies z = 0, x² + y² = 1, x + y + z = 3.

Resolução

a) Pela equação da esfera dada, temos

Utilizando as coordenadas polares, isto é, x = r cos q e y = r cos q , e considerando somente o valor positivo de z, obtemos

As variações de r e q são dadas por

Substituindo estes valores na fórmula de volume, obtemos

onde multiplicamos por 2, pois consideramos somente o valor positivo de z.

Utilizando o comando "Integrate", temos

In[ ]:= 2 Integrate[r Sqrt[a^2- r^2],{r,0,a},{theta,0,2 Pi}]
Out[ ]=

Como a > 0, concluímos que o volume da esfera de raio a é dado por V = u.v..

b) É dado que x + y + z = 3, daí substituindo x = r cos q e y = r sen q , achamos o valor de z:

A equação x² + y² = 1 nos dá as variações de r e q :

 Substituindo estes valores na fórmula de volume, obtemos

Utilizando o comando "Integrate", temos

In[ ]:= Integrate[r (3-r Cos[theta]-r Sin[theta]),{r,0,1},{theta,0,2 Pi}]
Out[ ]= 3 Pi

Logo, concluímos que o volume do sólido é dado por V = 3p u.v..

5.4.2.2 Coordenadas cilíndricas

As mudanças de variáveis de coordenadas cartesianas para coordenadas cilíndricas são dadas por

com z = g(r,q ), r ³ 0, 0 £ q £ 2p .

Ao invés de usar o elemento de volume dV(xyz) = dz dy dx, podemos usar o elemento dado por dV(rq z) = r dr dq dz. Assim, temos a seguinte fórmula de cálculo de volume:

Utilizando os comando do Mathematica a fórmula dada acima é representada por "Abs[Integrate[r,{r,0,a}, {theta,0,2 Pi},{z,g1(r,theta),g2(r,theta )}]], isto é,

V =

Utilizamos o comando "Abs" antes do comando "Integrate" para ter valor absoluto do resultado, pois o volume sempre é um valor positivo.

A seguir damos alguns exemplos de cálculo de volume em coordenadas cilíndricas utilizando a integração tripla.

Exemplo 5.15

a) Calcular o volume da esfera de raio "a" utilizando coordenadas cilíndricas;
b) Calcular o volume do sólido limitado pelo cilindro x² + y² = 9 e os planos z =1, x + z = 5.

Resolução

a) A equação de esfera de raio a é dada por x² + y² + z² = a². Substituindo os valores de x, y e z em coordenadas cilíndricas, obtemos z² = a² - r², daí calculamos as variações de z como sendo

e, as variações de r e q são dadas por 0 £ r £ a e 0 £ q £ 2p , respectivamente. Assim, a integral para o cálculo de volume é dada por

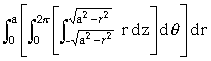Utilizando o comando "Integrate", podemos calcular o volume desejado:

In[ ]:= Integrate[r,{r,0,a},{theta,0,2 Pi},{z,-Sqrt[a^2-r^2],Sqrt[a^2-r^2]}]
Out[ ]=

Como a > 0, concluímos que o volume da esfera de raio a é dado por V = u.v..

b) No plano xy o cilindro x² + y² = 9 torna-se circunferência. Substituindo os valores de x e y em coordenadas cilíndricas, obtemos as variações de r e q como seguem:

 As variações de z já são dadas, isto é,

Assim, a integral para o cálculo de volume é dada por

Utilizando o comando "Integrate" podemos calcular o volume desejado:

In[ ]:= Integrate[r,{r,0,3},{theta,0,2 Pi},{z,1,5- r Cos[theta]}]
Out[ ]= 36 Pi

Logo, concluímos que o volume desejado é dado por 36p u.v..

5.4.3 Volume de um sólido em coordenadas esféricas

Nesta subseção apresentamos o cálculo de volume de um sólido cujas equações são dadas em coordenadas esféricas. As mudanças de variáveis de coordenadas cartesianas para coordenadas esféricas são dadas por

com r ³ 0, 0 £ q £ 2p , 0 £ f £ p .

Ao invés de usar o elemento de volume dV(xyz) = dz dy dx, podemos usar o elemento dado por dV(rq f )= r² sen f dr dq df . Assim, temos a seguinte fórmula de cálculo de volume:

Utilizando os comandos do Mathematica, a fórmula dada acima é dada por "Integrate[r^2 Sin[phi],{r,0,a},{theta,0,2 Pi},{phi,0,Pi}]", isto é,

A seguir damos um exemplo de cálculo de volume em coordenadas esféricas utilizando a integração tripla:

Exemplo 5.16

Calcular o volume da esfera de raio "a" utilizando coordenadas esféricas.

Resolução

Em coordenadas esféricas as variações de r, q , f de uma esfera de raio "a" são dadas por

Utilizando o comando "Integrate", temos o resultado desejado:

In[ ]:= Integrate[r^2 Sin[phi],{r,0,a},{theta,0,2 Pi},{phi,0,Pi}]

Out[ ]=

Logo, concluímos que o volume de uma esfera de raio a é dado por V = u.v..

5.4.4 Volume de um sólido de revolução

Nesta seção apresentamos o volume de um sólido obtido pela rotação de uma curva em torno de um eixo fixo ou um a reta dada. Também calculamos a área da superfície obtida pela rotação.

O volume do sólido de revolução obtido por revolução da região limitada pelo gráfico de y = f(x), x = a, x = b, e o eixo x em torno do eixo x é dado por

e em torno do eixo y, é dado por

A fórmula para o cálculo de volume de um sólido de revolução em torno do eixo x utilizando Mathematica é dada por "Pi Integrate[f[x]^2, {x,a,b}]", isto é,

e em torno do eixo y, é dado por "2 Pi Integrate[x f[x],{x,a,b}]", isto é,

O volume do sólido de revolução obtido por revolução da região limitada pelo gráfico de x = g(y), y = c, y = d, e o eixo y em torno do eixo y é dado por

e em torno do eixo x, é dado por

A fórmula para o cálculo de volume de um sólido de revolução em torno do eixo y utilizando Mathematica é dada por " Pi Integrate[g[y]^2, {y,c,d}]", isto é,

 e em torno do eixo x, é dado por "2 Pi Integrate[y g[y],{y,c,d}]"

A seguir damos alguns exemplos de cálculo de volume de um sólido de revolução:

Exemplo 5.17

a) Encontrar o volume do sólido gerado pela rotação em torno do eixo dos x, da região limitada pela curva y = x² + x - 3, o eixo x e as retas x = - 3 e x = 3;

b) Encontrar o volume do sólido gerado pela rotação em torno do eixo x, da região entre o gráfico da função y = sen x e o eixo x, de 0 a 2p .

c) Encontrar o volume do sólido gerado pela rotação da região entre o gráfico da função y = x³, - 1 £ x £ 1

i) em torno do eixo x;
ii) em torno do eixo y.

Resolução

Para gerar o sólido de revolução carregamos o pacote desejado utilizando o seguinte comando:

In[ ]:= Needs["Graphics`SurfaceOfRevolution`"]

Podemos obter também a mesma figura tridimensional de um sólido de revolução da função y = f(x), a £ x £ b, em torno do eixo x utilizando o comando "ParametricPlot3D" da seguinte forma:

In[ ]:= ParametricPlot3D[{x,f[x] Cos[theta], f[x] Sin[theta]}, {x,a,b},{theta,0,2 Pi}]

Quando a revolução é em torno do eixo y da função y = f(x), a £ x £ b, o comando utilizado é o seguinte:

In[ ]:= ParametricPlot3D[{x Cos[theta],x Sin[theta], f[x]},{x,a,b},{theta,0,2 Pi}]

A seguir resolvemos os exemplos dados construindo os sólidos e calculando as integrais necessárias.

a) In[ ]:= Plot[x^2+x-3,{x,-3,3}]

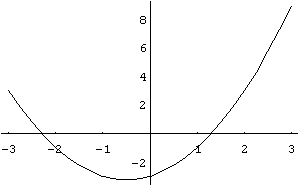
Out[ ]= -Graphics-

In[ ]:= SurfaceOfRevolution[x^2+x-3,{x,-3,3}, Axis->{1,0,0}]
ou
In[ ]:= f[x_]:= x^2+x-3
        ParametricPlot3D[{x,f[x] Cos[t],f[x] Sin[t]}, {x,-3,3},{t,0,2 Pi}]

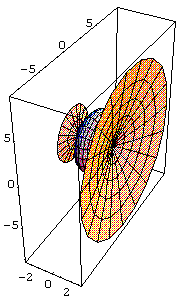
Out[ ]= -Graphics3D-

In[ ]:= Pi Integrate[(x^2+x- 3)^2,{x,- 3,3}]
Out[ ]=

Logo, concluímos que o volume desejado é V = u.v..

b) In[ ]:= Plot[Sin[x],{x,0,2 Pi}]

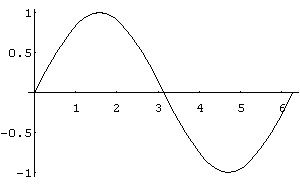
Out[ ]= -Graphics-

In[ ]:= SurfaceOfRevolution[Sin[x],{x,0,2Pi}, Axis->{1,0,0}]
ou
In[ ]:= Clear[f]
        f[x_]:= Sin[x]
        ParametricPlot3D[{x,f[x] Cos[t],f[x] Sin[t]}, {x,0,2 Pi},{t,0,2 Pi}]

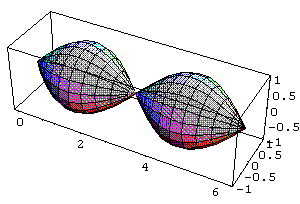
Out[ ]= -Graphics3D-

In[ ]:= Pi Integrate[(Sin[x])^2,{x,0,2 Pi}]
Out[ ]= Pi²

Logo, o volume desejado é V = p ² u.v..

c) In[ ]:= Plot[x^3,{x,- 1,1},PlotRange->{- 1,1}]

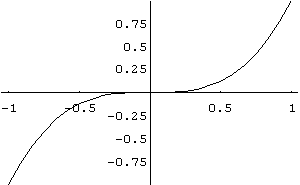
Out[ ]= -Graphics-

A seguir faremos separadamente os gráficos e os cálculos para cada eixo:

c) i) Cálculos com rotação em torno do eixo x

Inicialmente apresentamos o gráfico tridimensional utilizando os comandos "SurfaceOfRevolution" e "ParametricPlot3D". Veja a seguir que os dois comandos geram o mesmo gráfico:

In[ ]:= SurfaceOfRevolution[x^3,{x,- 1,1},Axis->{1,0,0}]
ou
In[ ]:= f[x_]:= x^3
        ParametricPlot3D[{x,f[x] Cos[t],f[x] Sin[t]}, {x,-1,1},{t,0,2 Pi}]

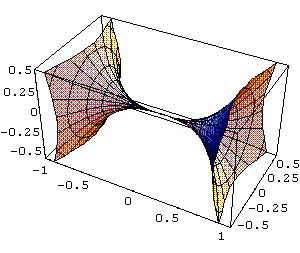
Out[ ]= -Graphics3D-

In[ ]:= Pi Integrate[(x^3)^2,{x,- 1,1}]

Out[ ]=

Logo, o volume desejado é V = u.v..

c) ii) Cálculos com rotação em torno do eixo y

Inicialmente apresentamos o gráfico tridimensional utilizando os comandos "SurfaceOfRevolution" e "ParametricPlot3D". Veja a seguir, que os dois comandos geram o mesmo gráfico:

In[ ]:= SurfaceOfRevolution[x^3,{x,- 1,1},Axis->{0,0,1}]
ou
In[ ]:= ParametricPlot3D[{x Cos[t],x Sin[t],x^3},{x,- 1,1},{t,0,2 Pi}]

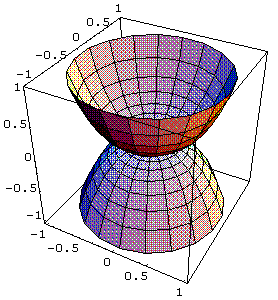
Out[ ]= -Graphics3D-

In[ ]:= 2 Pi Integrate[x x^3,{x,- 1,1}]
Out[ ]=

Logo, o volume desejado é V = u.v..

Observações

• Na utilização do comando "ParametricPlot3D" não necessitamos de nenhum pacote.

• Podemos traçar os sólidos de revolução em torno dos dois ou três eixos ao mesmo tempo. Veja a seguir alguns exemplos dessas combinações:

- Exemplo anterior, item a), com rotação em torno dos eixos x e z:

In[ ]:= SurfaceOfRevolution[x^2+x- 3,{x,- 3,3}, Axis->{1,0,1}]

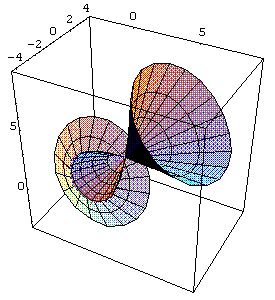
Out[ ]= -Graphics3D-

- Exemplo anterior, item a), com rotação em torno dos eixos x, y e z:

In[ ]:= SurfaceOfRevolution[x^2+x- 3,{x,- 3,3}, Axis->{1,1,1}]

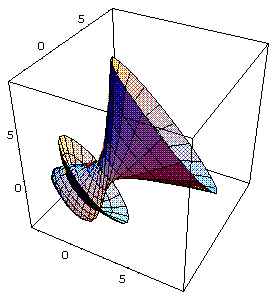
Out[ ]= -Graphics3D-