Let
Let ![]() be a sequence of discrete finite random variables. The entropy rate
is defined as
be a sequence of discrete finite random variables. The entropy rate
is defined as
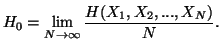
In general ![]() doesn't exist. Here we shall give conditions for evaluating its value.
This is based on well known statistical concepts famous as stationary
random variables
and Markov Chain.
doesn't exist. Here we shall give conditions for evaluating its value.
This is based on well known statistical concepts famous as stationary
random variables
and Markov Chain.
Definition 1.1. (Stationary). A sequence of RV's ![]() is said to be stationary if the joint probability distributions
are invariant under the transition of time origin i.e.,
is said to be stationary if the joint probability distributions
are invariant under the transition of time origin i.e.,
|
|
(1.10) |
Definition 1.2. (Markov Chain) A sequence of random variables ![]() is said to be Markov Chain if for every N, the RV
is said to be Markov Chain if for every N, the RV ![]() is conditionally independent of
is conditionally independent of ![]() given
given ![]() i.e.,
i.e.,
|
|
(1.11) |
Based on the above definitions the following property holds.
Property 1.62. If the sequence of random variables is stationary, we have
![]()
Moreover, the following property holds.
Property 1.63. The entropy rate of a stationary Markov sequence ![]() is given by
is given by
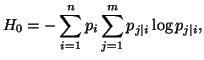
Note 1.5. The expression ![]() given in the property 1.63 is famous as "Markov Entropy".
given in the property 1.63 is famous as "Markov Entropy".