Go to:Table of Contents

Entropy of a Continuous Random Variable

Shannon's entropy though defined for a discrete random variable can be extended to situations when the random variable under consideration is continuous.

Let X be a continuous random variable with probability density function $p(x)$ on I, where$I=(-\infty,\infty)$, then the entropy is given by

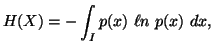$$H(X)=-\int_{I}{p(x)\ \ell n\ p(x)\ dx},$$ (1.13)

whenever it exists. The measure (1.13) sometimes called "differential entropy". It has many of the properties of discrete entropy but unlike the entropy of a discrete random variable that of a continuous random variable may be infinitely large, negative or positive (Ash, 1965 [6]). The entropy of a discrete random variable remains invariant under a change of variable, however with a continuous random variable the entropy does not necessarily remain invariant.