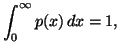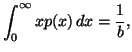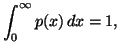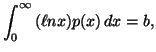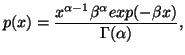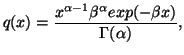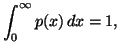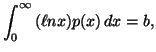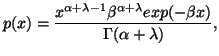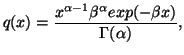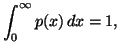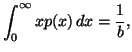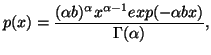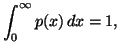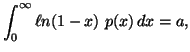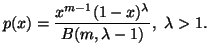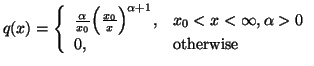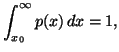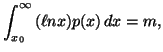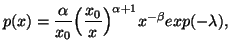In Chapter 1, we saw that the "principle of maximum entropy"
is applicable in situations where information becomes available in the
form of expected value or constraints and we wish to determine the underlying
probability density. This restriction on the form of available information
limits the type of problem which we can consider; the principle being applicable
only if the partial information is in the form of averages.
First, as example, consider a situation where we have partial information in the form of averages and also that the prior estimate of the probability distribution is say the Poisson distribution with a certain value of the parameter which is the mean. This problem cannot be handled by M.E.P. If we were to apply the M.E.P. we would not be able to use the partial information which is coded in the estimate of the unknown distribution.
This serious limitation of M.E.P. cannot in general be relaxed. However,
the problem can be handled in situations when some prior knowledge about
the underlying distribution is known in addition to the partial information
in the form of averages. This leads to the minimum relative information
principle given as follows:
When a prior distribution, that estimates the underlying density
, is known in addition to some constraints; then of all the densities
which satisfy the constraints we should select underlying probability density as that which yields the minimum relative information.
Given a prior density ![]() ,
we wish to arrive at a density function
,
we wish to arrive at a density function ![]() ,
when this underlying density function
,
when this underlying density function![]() satisfies the usual probability constraint.
satisfies the usual probability constraint.
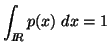 |
(2.12) |
and the partial informations in the form of averages
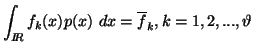 |
(2.13) |
By the minimum P.R.I. ![]() is to be such that it minimizes (2.9) subject to the constraints (2.10)
and (2.11).
is to be such that it minimizes (2.9) subject to the constraints (2.10)
and (2.11).
Using Lagrange's method of multipliers, we have
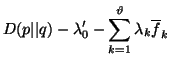
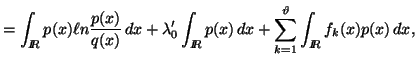 |
(2.14) |
where ![]() are constants.
are constants.
Equating the variations of this quantity with respect to ![]() to zero, we obtain
to zero, we obtain
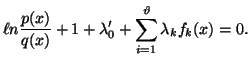 |
(2.15) |
This yields
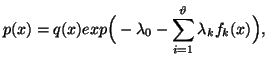 |
(2.16) |
where![]() .
Thus we have
.
Thus we have
(i)![]() .
.
(ii) ![]() .
.
Next we show that ![]() obtained in (2.16) does indeed yield the M.R.I. and that it is unique.
obtained in (2.16) does indeed yield the M.R.I. and that it is unique.
The following property give some examples of the minimum relative information principle including the discrete case too.
Property 2.18. We have
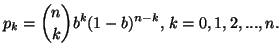
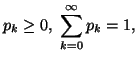
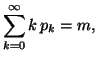
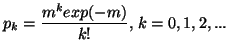
![$\displaystyle q(x)={1\over \sigma\sqrt{2\pi}}exp \Big[-{(x-y)^2\over2\sigma^2}\Big],$](img592.gif)
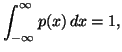
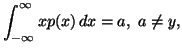
![$\displaystyle p(x)={1\over \sigma\sqrt{2\pi}}exp \Big[-{(x-b)^2\over2\sigma^2}\Big],$](img595.gif)
![$\displaystyle q(x)={1\over \sigma\sqrt{2\pi}}exp \Big[-{(x-y)^2\over2\sigma^2}\Big],$](img592.gif)
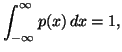
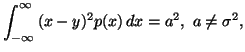
![$\displaystyle p(x)={1\over a\sqrt{2\pi}}exp \Big[-{(x-y)^2\over 2a^2}\Big],$](img598.gif)
![$\displaystyle q(x)={1\over \sigma\sqrt{2\pi}}exp \Big[-{(x-y)^2\over2\sigma^2}\Big],$](img592.gif)
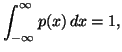
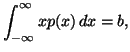
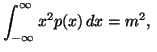 where
where![$\displaystyle p(x)={1\over a\sqrt{2\pi}}exp \Big[-{(x-b)^2\over2a^2}\Big],$](img603.gif)