Next:Important
ObservationsUp:Characterizations
of Generalized Entropies
Previous:Entropy
of Kind Go to:Table
of Contents
Entropy of Order r and
Degree s
Sharma and Mittal (1975) [90] presented an
axiomatic characterization of entropy of order 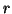 and degree
and degree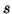 .
It is based on the Rényi's approach, where the additivity property
has been changed (generally referred as nonadditivity).
.
It is based on the Rényi's approach, where the additivity property
has been changed (generally referred as nonadditivity).
Let 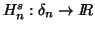 be a real valued continuous function satisfying
be a real valued continuous function satisfying
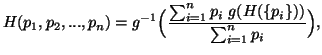
where g is a strictly monotonic continuous function, and 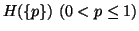 is the self-information of an event of a probability distribution
is the self-information of an event of a probability distribution 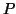 satisfying:
satisfying:
-
(i)
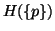 is a continuous function
is a continuous function 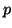 in (0,1].
in (0,1].
-
(ii)
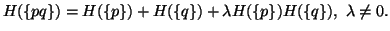
-
(iii)
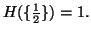
Then
![$\displaystyle H(p_1,p_2,...,p_n;1,s)=(2^{1-s}-1)^{-1}\Big[ \exp_2\Big((s-1){\sum_{i=1}^n{p_i\log_2 p_i}\over\sum_{i=1}^n{p_i}}\Big)-1\Big],\ s\neq 1,\ s>0$](img855.gif)
|
|
|
(3.20) |
and
![$\displaystyle H(p_1,p_2,...,p_n;r,s)=(2^{1-s}-1)^{-1}\Big[\Big({\sum_{i=1}^n{p......r \sum_{i=1}^n{p_i}}\Big)^{s-1\overr-1}-1\Big],\ r\neq 1,\ s\neq 1,\ r>0,\ s>0$](img856.gif)
|
|
|
(3.21) |
Van der Pyl (1977) [118]restructured the
above axiomatic system and considered as follows:
Let 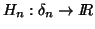 be a real valued continuous function satisfying the following:
be a real valued continuous function satisfying the following:
-
(i)
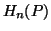 is a symmetric function of its arguments.
is a symmetric function of its arguments.
-
(ii)
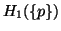 is continuous in (0,1].
is continuous in (0,1].
-
(iii)
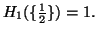
-
(iv) There is a sequence
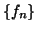 such that
such that
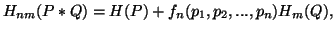
for all 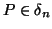 ,
, 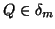 and
and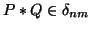 .
.
-
(v) There exists a strictly monotonic continuous function g such that
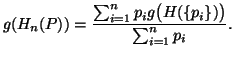
Then the above set of axioms lead to the measures (3.20) and (3.21).
Picard (1979) [77] extended the above
set of axioms by introducing the idea of weights or preferences and came
up with the weighted entropies given in section 3.6.2.
The measure (3.21) can be characterized in a much more simplified form
given as follows:
Let 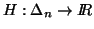 be a real valued continuous function satisfying the following axioms:
be a real valued continuous function satisfying the following axioms:
-
(i)
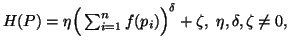 where f is a continuous function defined on [0,1].
where f is a continuous function defined on [0,1].
-
(ii)
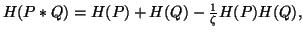 for
for 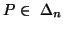 ,
, 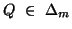 and
and 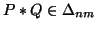 .
.
-
(iii)
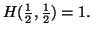
Then
![$\displaystyle H(P)=( 2^{(1-\sigma )^\delta}-1)^{-1}\Big[\Big(\sum_{i=1}^n{p^\sigma_i}\Big)^\delta -1\Big],\\sigma>0, \ \delta\neq 0,$](img868.gif) that is same as (3.21) for
that is same as (3.21) for 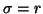 and
and 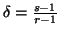 ,
with
,
with 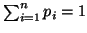 .
.
21-06-2001
Inder Jeet Taneja
Departamento de Matemática - UFSC
88.040-900 Florianópolis, SC - Brazil
![]() be a real valued continuous function satisfying
be a real valued continuous function satisfying
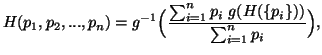
![]() is the self-information of an event of a probability distribution
is the self-information of an event of a probability distribution ![]() satisfying:
satisfying:
![$\displaystyle H(p_1,p_2,...,p_n;1,s)=(2^{1-s}-1)^{-1}\Big[ \exp_2\Big((s-1){\sum_{i=1}^n{p_i\log_2 p_i}\over\sum_{i=1}^n{p_i}}\Big)-1\Big],\ s\neq 1,\ s>0$](img855.gif)
![$\displaystyle H(p_1,p_2,...,p_n;r,s)=(2^{1-s}-1)^{-1}\Big[\Big({\sum_{i=1}^n{p......r \sum_{i=1}^n{p_i}}\Big)^{s-1\overr-1}-1\Big],\ r\neq 1,\ s\neq 1,\ r>0,\ s>0$](img856.gif)
![]() be a real valued continuous function satisfying the following:
be a real valued continuous function satisfying the following:
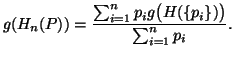
![]() be a real valued continuous function satisfying the following axioms:
be a real valued continuous function satisfying the following axioms:
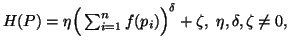 where f is a continuous function defined on [0,1].
where f is a continuous function defined on [0,1].![$\displaystyle H(P)=( 2^{(1-\sigma )^\delta}-1)^{-1}\Big[\Big(\sum_{i=1}^n{p^\sigma_i}\Big)^\delta -1\Big],\\sigma>0, \ \delta\neq 0,$](img868.gif)