The measure of uncertainty
The measure of uncertainty ![]() given by (1.7) satisfy many interesting properties. For simplicity, we
shall take
given by (1.7) satisfy many interesting properties. For simplicity, we
shall take ![]() or
or ![]() instead of
instead of ![]() .
Unless otherwise specified, it is understood that
.
Unless otherwise specified, it is understood that ![]()
![]()
![]() and
and ![]()
![]()
![]()
![]() .
Also it is understood that
.
Also it is understood that ![]() and all the logarithms are with base 2.
and all the logarithms are with base 2.
Property 1.1. (Nonnegativity). ![]() with equality iff
with equality iff ![]() ,
where
,
where![]()
![]() .
.
Property 1.2. (Continuity). ![]() is a continuous function of P.
is a continuous function of P.
Property 1.3. (Symmetry). ![]() is a symmetric function of its arguments, i.e.,
is a symmetric function of its arguments, i.e.,
Property 1.4. (Expansible). We have
Property 1.5. (Decisive). We have
Property 1.6. (Normality). We have
Property 1.7. (Sum Representation). We can write
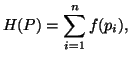
Property 1.8. (Recursivity). We have
Property 1.9. (Additivity). We have
![]()
Property 1.10. (Strongly Additive). We have
![]()
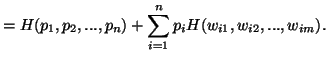
![]()
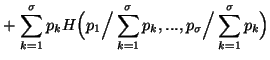
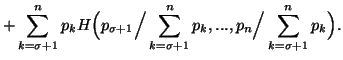
Property 1.12. (Generalized Grouping). We have
![]()
![]()
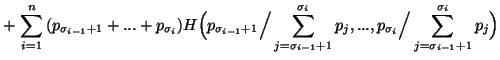
Property 1.13. (Binary-Entropic). Let
|
|
(1.8) |
Then
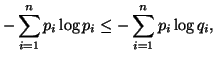 |
(1.9) |
with equality iff ![]() or iff
or iff ![]() (whenever
(whenever![]() for some
for some ![]() ,
the corresponding
,
the corresponding ![]() is also zero).
is also zero).
Property 1.15. (Maximality).![]() is maximum when all the probabilities are equal i.e.,
is maximum when all the probabilities are equal i.e.,
Property 1.16. (Uniform distribution). Let
![]()
![]()
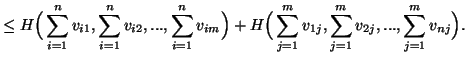
Property 1.18. (Independence Inequality). If
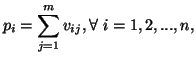
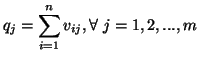
Property 1.19. (Concavity).![]() is a concave function of
is a concave function of ![]() in
in ![]() .
.
Property 1.20. (Schur-concavity).![]() is a Shur-concave function of
is a Shur-concave function of ![]() in
in ![]() .
.
Property 1.21. Let ![]() be a probability distribution such that
be a probability distribution such that ![]() .
Let us define
.
Let us define ![]() such that
such that ![]() Then
Then ![]() .
.
Property 1.22. (Difference among two entropies). If
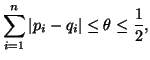
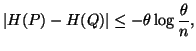
Property 1.23. Bounds on H(P). For ![]() ,
we have
,
we have
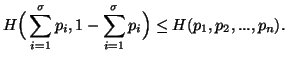
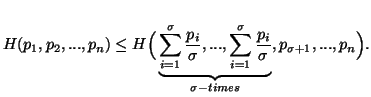
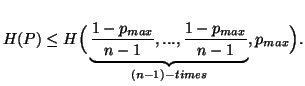
Property 1.26. If ![]() is strongly additive (property 1.10), then it is additive (property 1.9).
is strongly additive (property 1.10), then it is additive (property 1.9).
Property 1.27. If ![]() is additive (property 1.9) for
is additive (property 1.9) for ![]() and is expansible (property 1.4), then it is also additive (property 1.9).
and is expansible (property 1.4), then it is also additive (property 1.9).
Property 1.28. If ![]() is expansible (property 1.4) and strongly additive (property 1.10), then
it is recursive (property 1.8).
is expansible (property 1.4) and strongly additive (property 1.10), then
it is recursive (property 1.8).
Property 1.29. If ![]() is recursive (property 1.8) for
is recursive (property 1.8) for ![]() and symmetric (property 1.3) for
and symmetric (property 1.3) for ![]() ,
then it is symmetric (property 1.3) for
,
then it is symmetric (property 1.3) for ![]() and decisive (property 1.5).
and decisive (property 1.5).
Property 1.30. If ![]() is recursive (property 1.8), symmetric (property 1.3) for
is recursive (property 1.8), symmetric (property 1.3) for ![]() ,
then it is symmetric (property 1.3) and expansible (property 1.4).
,
then it is symmetric (property 1.3) and expansible (property 1.4).
Property 1.31. If ![]() is symmetric (property 1.3) and recursive (property 1.8), then
is symmetric (property 1.3) and recursive (property 1.8), then
Property 1.33. If ![]() is expansible (property 1.4) and subadditive (property 1.17) for
is expansible (property 1.4) and subadditive (property 1.17) for ![]() ,
then it is nonnegative (property 1.1).
,
then it is nonnegative (property 1.1).
Property 1.34. If ![]() is branching of the form
is branching of the form
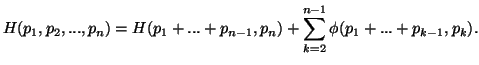
Property 1.35. If ![]() is recursive (property 1.8), and
is recursive (property 1.8), and ![]() ,
then
,
then
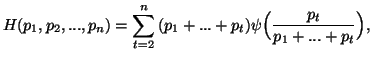
Property 1.36. If ![]() is normalized (property 1.6), symmetric (for
is normalized (property 1.6), symmetric (for ![]() )
(property 1.3) and recursive (for
)
(property 1.3) and recursive (for ![]() )
(property 1.8), then the function
)
(property 1.8), then the function ![]() satisfies the property 1.13(i)-(iv).
satisfies the property 1.13(i)-(iv).
Property 1.37. Binary entropic properties given by 1.13(i)-(iv)
implies that ![]() is symmetric (property 1.3), normalized (property 1.6), expansible (property
1.4), decisive (property 1.5), recursive (property 1.8), strongly additive
(property 1.9) and additive (property 1.10).
is symmetric (property 1.3), normalized (property 1.6), expansible (property
1.4), decisive (property 1.5), recursive (property 1.8), strongly additive
(property 1.9) and additive (property 1.10).
Note 1.1. Some of the properties given above can be seen in
Aczél and Daróczy (1975) [2]
and Mathai and Rathie (1975) [71]