Next:Dimensional
Unified Arithmetic andUp:Dimensional
Unified Divergence Measures
Previous:Dimensional
Unified Information RadiiGo to:Table
of Contents
M-Dimensional Unified
(r,s)-J-Divergences
The three different ways of defining 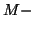 dimensional
unified
dimensional
unified 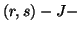 divergence
measures
are given by
divergence
measures
are given by
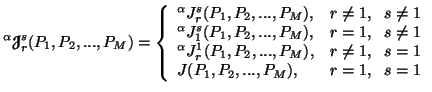
|
|
|
(5.18) |
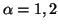 and 3, where for
and 3, where for 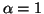 ,
we have
,
we have
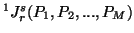
![$\displaystyle =(1-2^{1-s})^{-1}\Big\{\Big[ \sum_{i=1}^n{\Big(\sum_{{j,k=1}_......}}^M{\lambda_j\lambda_k}}\Big)\Big]^{s-1\over r-1}-1\Big\},\r\neq 1,\ s\neq 1$](img1163.gif)
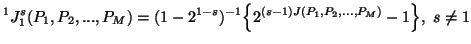 and
and
![$\displaystyle ^1 J^1_r(P_1,P_2,...,P_M)=(r-1)^{-1} log_2\Big[\sum_{i=1}^n{ \B......_{ji}p^{1-r}_{ki}}/ \sum_{{j,k=1}_{j\neqk}}^M{\lambda_j \lambda_k}\Big)}\Big]$](img1165.gif) For
For 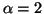 ,
we have
,
we have
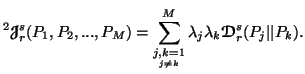
|
|
|
(5.19) |
For 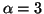 ,
we have
,
we have
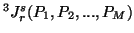
![$\displaystyle = (1-2^{1-s})^{-1}\Big\{ \Big[\sum_{i=1}^n{\Big(\sum_{j=1}^M{\l......^{\lambda_k}_{ki}}\Big)^{1-r}} \Big]^{s-1\overr-1}-1\Big\},\ r\neq 1, s\neq 1$](img1168.gif)
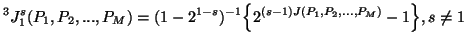
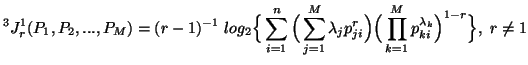 In particular, we have
In particular, we have
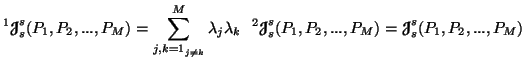 where
where
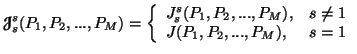 with
with
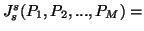
![$\displaystyle (1-2^{1-s})^{-1}\Big\{ \Big[\sum_{i=1}^n{\Big(\sum_{{j,k=1}_{j\....../ \sum_{{j,k=1}_{j\neq k}}^M{\lambda_j\lambda_k}\Big)}\Big]-1\Big\},\ s\neq 1$](img1174.gif)
For two dimensional case, i.e., when M=2,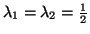 ,
, 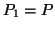 and
and 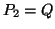 ,
we have
,
we have
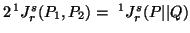
![$\displaystyle = 2(1-2^{1-s})^{-1}\Big\{\Big[\sum_{i=1}^n{\Big({p^r_iq^{1-r}_i+p^{1-r}_iq^r_i\over2}\Big)} \Big]^{s-1\over r-1}-1\Big\},$](img1176.gif)
|
|
|
(5.20) |
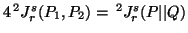
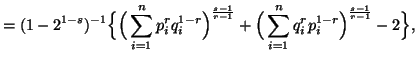
|
|
|
(5.21) |
and
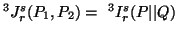
![$\displaystyle = (1-2^{1-s})^{-1}\Big\{ \Big[ \sum_{i=1}^n{ \Big( {p^{1+r\over2......+ p^{1+r\over 2}_i q^{1-r\over 2}_i\over 2}\Big)}\Big]^{s-1\over r-1}-1\Big\},$](img1180.gif)
|
|
|
(5.22) |
for all 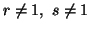 .
.
Note 5.3. The measures (5.20) and (5.21) is as given by (4.11)
and (4.7). While the measure (5.22) is new.
21-06-2001
Inder Jeet Taneja
Departamento de Matemática - UFSC
88.040-900 Florianópolis, SC - Brazil
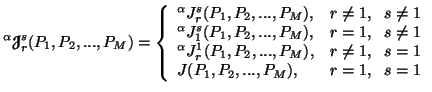
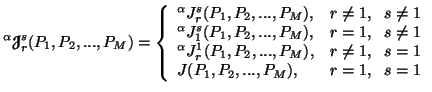
![]() and 3, where for
and 3, where for ![]() ,
we have
,
we have
![]()
![$\displaystyle =(1-2^{1-s})^{-1}\Big\{\Big[ \sum_{i=1}^n{\Big(\sum_{{j,k=1}_......}}^M{\lambda_j\lambda_k}}\Big)\Big]^{s-1\over r-1}-1\Big\},\r\neq 1,\ s\neq 1$](img1163.gif)
![$\displaystyle ^1 J^1_r(P_1,P_2,...,P_M)=(r-1)^{-1} log_2\Big[\sum_{i=1}^n{ \B......_{ji}p^{1-r}_{ki}}/ \sum_{{j,k=1}_{j\neqk}}^M{\lambda_j \lambda_k}\Big)}\Big]$](img1165.gif)
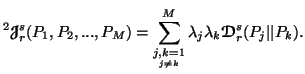
![]() ,
we have
,
we have
![]()
![$\displaystyle = (1-2^{1-s})^{-1}\Big\{ \Big[\sum_{i=1}^n{\Big(\sum_{j=1}^M{\l......^{\lambda_k}_{ki}}\Big)^{1-r}} \Big]^{s-1\overr-1}-1\Big\},\ r\neq 1, s\neq 1$](img1168.gif)
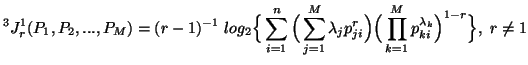
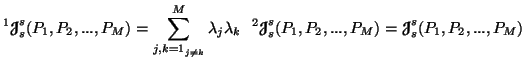
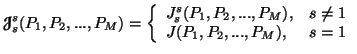
![]()
![$\displaystyle (1-2^{1-s})^{-1}\Big\{ \Big[\sum_{i=1}^n{\Big(\sum_{{j,k=1}_{j\....../ \sum_{{j,k=1}_{j\neq k}}^M{\lambda_j\lambda_k}\Big)}\Big]-1\Big\},\ s\neq 1$](img1174.gif)
![]() ,
, ![]() and
and ![]() ,
we have
,
we have
![]()
![$\displaystyle = 2(1-2^{1-s})^{-1}\Big\{\Big[\sum_{i=1}^n{\Big({p^r_iq^{1-r}_i+p^{1-r}_iq^r_i\over2}\Big)} \Big]^{s-1\over r-1}-1\Big\},$](img1176.gif)
![]()
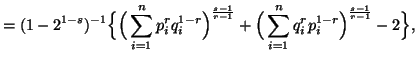
![]()
![$\displaystyle = (1-2^{1-s})^{-1}\Big\{ \Big[ \sum_{i=1}^n{ \Big( {p^{1+r\over2......+ p^{1+r\over 2}_i q^{1-r\over 2}_i\over 2}\Big)}\Big]^{s-1\over r-1}-1\Big\},$](img1180.gif)