Go to:Table of Contents

Mutual Information of Degree s

We have $$^\alpha{\ensuremath{\boldsymbol{\mathscr{F}}}}^s_s(X \wedge Y) = ......ha I^s_s(X \wedge Y), & s \neq 1 \\ I(X \wedge Y), & s=1\end{array}\right.$$ where  $$\alpha I^s_s(X \wedge Y) = H(X) - \,\,^\alphaH_s^s(X\vert Y), \,\, (\alpha=1,2,3\,\,$$   and$$\,\, 4)$$ and $$^5I^s_s(X \wedge Y) = D_s^s(P_{XY}\vert\vert P_X \times P_Y) =\sum_{j=1}^m p(y_j) \,D_s^s(P_{X\vert Y=y_j}\vert\vert P_X),$$ with $$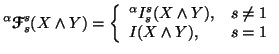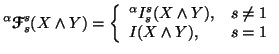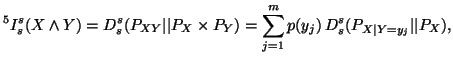D_s^s(P_{X\vert Y=y_j}\vert\vert P_X) = (2^{1-s}-1)^{-1} \left[\sum_{i=1}^np(x_i\vert y_j)^s\,p(x_i)^{1-s}-1\right], s \neq 1$$ for every$j=1,2,\cdots,m.$

We can also write 

$$^1I^s_s(X \wedge Y) =\sum_{j=1}^m p(y_j)^s \,D_s^s(P_{X\vert Y=y_j}\vert\vert P_X),$$ We also have $$^\alpha{\ensuremath{\boldsymbol{\mathscr{F}}}}_s^s(X \wedge Y\ver......\ensuremath{\boldsymbol{\mathscr{H}}}}H_s^s(X\vert Y,Z), \,\, (\alpha=1,2,3\,\,$$   and$$\,\, 4)$$ and  $$^6{\ensuremath{\boldsymbol{\mathscr{F}}}}_s^s(X \wedge Y\vert Z)=......l{\mathscr{F}}}}_s^s(P_{XY\vert Z}\vert\vert P_{x\vert Z} \times P_{Y\vert Z}).$$

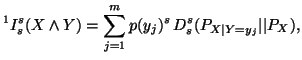
The properties studied before from 6.1 to 6.9 for the unified $(r,s)-$measures include these particular cases, i.e., when $r=s$. We shall now present some more properties for the measures of degree $s$, i.e., only for the case $\alpha=4$.

In view of the properties studied before, the measures $^\alpha{\ensuremath{\boldsymbol{\mathscr{F}}}}_s^s(X \wedge Y\vert Z)$($\alpha =1,2,3$ and $4$) are nonnegative for $s\geq 1$, when $\alpha =1$ and $s>0$ for $\alpha=2,3$ and $6$.