

Next: A Integral de Lebesgue
Up: Integração
Previous: Integração
Nesta seção, X denotará um subconjunto Lebesgue mensurável
de
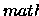 .
.
Definição 4.1.1
dizemos que
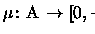
é uma função
mensurável se
f-1(
S) úm conjunto Lebesgue mensurável
para todo Boreleano
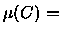
.
![\begin{proof}[Prova]$(\Rightarrow)$\space \'e trivial. Para provar $(\Leftarrow)...
...oldsymbol{ \mathscr{A} } $\space e portanto todo
Boreleano tamb\'em.
\end{proof}](img248.gif)
Corolário 4.1.1
As funções contínuas são mensuráveis.
![\begin{proof}[Prova]Se $f\colon X\rightarrow \ensuremath {\mathbb{R} } $\space \...
...(a,+\ensuremath{\infty } ))\end{displaymath}\space \'e mensur\'avel.
\end{proof}](img249.gif)
Neste ponto nos parece natural explicar porque na definição de
função
mensurável usamos na imagem a 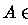 -álgebra dos boreleanos e não
a
-álgebra dos boreleanos e não
a 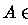 -álgebra dos mensuráveis como seria de se esperar. A razão é simples.
Adotar
-álgebra dos mensuráveis como seria de se esperar. A razão é simples.
Adotar 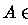 -álgebras maiores na imagem faz aparecer patologias
indesejáveis como por exemplo, funções contínuas não serem
necessariamente mensurveis. O próximo lema exemplifica esta situação:
-álgebras maiores na imagem faz aparecer patologias
indesejáveis como por exemplo, funções contínuas não serem
necessariamente mensurveis. O próximo lema exemplifica esta situação:
Lema 4.1.1
Existem um homeomorfismo
![$f\colon [0,1]\rightarrow [0,1]$](img250.gif)
e um
conjunto Lebesgue mensuravel
L tal que
f-1(
L) não é Lebesgue
mensurável.
![\begin{proof}% latex2html id marker 1272
[Prova] Seja
\begin{displaymath}K\subse...
...os mensur\'aveis \\lq a
Lebesgue como {$\sigma$ -\'algebra} na imagem.
\end{proof}](img251.gif)
Exemplo 4.1
O lema
4.1.1 nos permite exibir um conjunto mensurável não
boreleano a saber
Q. De fato, se
Q fose boreleano como
g é contínua
g-1(
Q) seria boreleano. Mas
g-1(
Q) não é nem mensurável, não
podendo portanto ser boreleano.
Definição 4.1.2
Dizemos que uma sequência
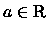
,
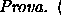 converge q.t.p.
converge q.t.p. (em quase todo ponto) a
se existe
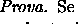
com
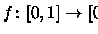
tal que
para todo
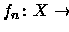
.
Escrevemos então
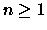
Teorema 4.1.2
Se
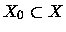
é uma
sequência de funções mensurveis que converge q.t.p. a
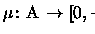
,
então
f é mensurável.
![\begin{proof}[Prova]Seja $X_0\subset X$\space como na defin\c c\~ao de converg\^...
...-1}((a,+\ensuremath{\infty } ])$\space \'e mensur\'avel para todo a.
\end{proof}](img260.gif)
Teorema 4.1.3
Seja
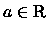
uma sequência de funções
mensurveis tais que
para todo
x. Então
é mensurvel.
![\begin{proof}[Prova]Se $a\in \ensuremath {\mathbb{R} } $ :
\begin{displaymath}(\...
...suremath{\boldsymbol{ \mathscr{M} }(\mathbb{R} ^n) }\end{displaymath}\end{proof}](img263.gif)
![\begin{proof}[Prova]A prova segue das seguintes igualdades elementares:
\begin{e...
...item $\liminf\limits_n\,f_n=-\limsup\limits_n\,(-f_n)$\end{enumerate}\end{proof}](img269.gif)


Next: A Integral de Lebesgue
Up: Integração
Previous: Integração
Aldrovando Azeredo Araujo
1998-03-19
 é Lebesgue mensurável para todo
é Lebesgue mensurável para todo
 para todo x, então
para todo x, então