

Next: About this document ...
Up: A Integral de Lebesgue
Previous: A Integral de Lebesgue
Seja
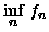 um conjunto Lebesgue mensurável. Sobre X podemos definir
uma
um conjunto Lebesgue mensurável. Sobre X podemos definir
uma 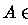 -álgebra e uma medida sobre esta
-álgebra e uma medida sobre esta 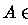 -álgebra como segue:
-álgebra como segue:
Definição 5.1.1
Denotamos por
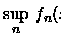
a família de subconjuntos
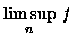
tal que existe
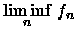
satisfazendo
Sobre
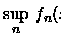
definimos a função que o leitor pode facilmente verificar ser
uma medida
vai
Como de fato 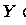 é a restrição de
é a restrição de
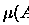 sobre os conjuntos
mensuráveis contidos em X, denotaremos
sobre os conjuntos
mensuráveis contidos em X, denotaremos
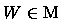 .
.
Definição 5.1.2
Se

é mensurável, definimos a
integral
de f (ou integral de Lebesgue) como:
onde o supremo é tomado sobre todos os conjuntos finitos

.
Naturalmente, o supremo pode ser
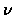 .
dada uma
.
dada uma
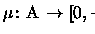 definimos suas partes positiva e negativa, f+ e f-, como
definimos suas partes positiva e negativa, f+ e f-, como
Então f=f++f-.
Definição 5.1.3
Definimos a
integral de
f como:
quando os dois termos a direita não são ambos
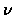 .
Neste caso
a integral
não está definida.
.
Neste caso
a integral
não está definida.
Definição 5.1.4
Dizemos que
f é
integrável se
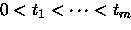 |
(5.1) |
Definição 5.1.5
Se
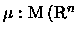
é um conjunto mensurável definimos a função
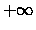
via:
que denomina-se de
função característica de A
As seguintes propriedades são elementares e portanto a prova será deixada ao
leitor:
Lema 5.1.1
São verdadeiras:
- 1.
-

- 2.
- Se
 ,
com
,
com  mensuráveis e
mensuráveis e
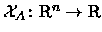 vale:
vale:
para toda
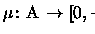 integrável ou
integrável ou  .
.
- 3.
- Se
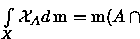 é integrável ou
é integrável ou 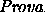 ,
e
,
e
então
![\begin{proof}[Prova]
Dados \ensuremath {0<t_1<\cdots<t_{n}} :
\begin{displaymath...
... limitadas
pela integral de $f$\space demonstrando assim o teorema.
\end{proof}](img300.gif)
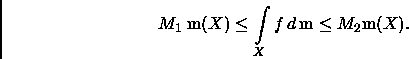
Teorema 5.1.2 (Convergência Monótona)
Seja
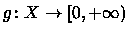
uma sequência de funções que converge
à função
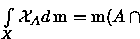
.
Então:
![\begin{proof}% latex2html id marker 1448
[Prova] Seja $X_0\subset X$\space com $...
...\int\limits_{X}\,f_n\,d\ensuremath{\mathfrak{m} }} .\end{displaymath}\end{proof}](img304.gif)
Teorema 5.1.3 (Lema de Fatou)
Seja
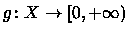
para
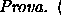
uma sequência de funções
integráveis. Então
![\begin{proof}% latex2html id marker 1567
[Prova] Seja
\begin{displaymath}F_n=\i...
... {\int\limits_{X}\,f_n\,d\ensuremath{\mathfrak{m} }}\end{displaymath}\end{proof}](img306.gif)
Agora relacionamos a integral de funções simples, isto é
funções da forma
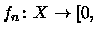 definidas por
definidas por
onde (Ai)i são disjuntos e mensuráveis, com a integral de uma função
f positiva.
Teorema 5.1.4
Seja
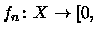
simples isto é
com
Então
g é integrável se e somente se
tal que
.
Neste caso

\end{proof}](img314.gif)
Teorema 5.1.5
Se
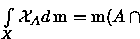
é mensurável, existe uma sequência de
funções simples
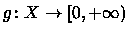
tal que
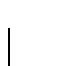
em todo
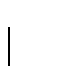
.
![\begin{proof}[Prova]Para cada $n$\space e $k=1,2\ldots,n2^n$\space seja
\begin{d...
...\end{displaymath}Finalmente $f_n$\space \'e simples para cada $n$ .
\end{proof}](img317.gif)
Segue do teorema 5.1.5 que se
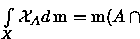 é integrável
então
é integrável
então
onde fn é definida como na prova do teorema.
Estamos finalmente prontos para provar que a integral é aditiva.
Corolário 5.1.1
Se
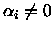
são integráveis entaão
af+
bg é integrável para todo

e
![\begin{proof}% latex2html id marker 1678
[Prova]Deixamos a cargo do leitor prova...
...th {\int\limits_{X}\,g\,d\ensuremath{\mathfrak{m} }}\end{displaymath}\end{proof}](img322.gif)
O próximo teorema é um dos teoremas mais importantes na teoria da integração.
Teorema 5.1.6 (Convergência Dominada)
Seja
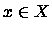
uma sequência de funções integráveis que
converge em q.t.p. a
. Então se existe
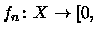
integrável tal que
f é integrável e
![\begin{proof}% latex2html id marker 1734
[Prova]Como $\ensuremath{ \left\vert f\...
...its_{X_0}\,f_n\,d\ensuremath{\mathfrak{m} }}\end{displaymath}\begin
\end{proof}](img327.gif)


Next: About this document ...
Up: A Integral de Lebesgue
Previous: A Integral de Lebesgue
Aldrovando Azeredo Araujo
1998-03-19
 é mensurável, definimos a integral
de f (ou integral de Lebesgue) como:
é mensurável, definimos a integral
de f (ou integral de Lebesgue) como:
 .
.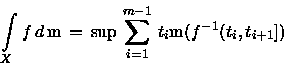

 ,
com
,
com  mensuráveis e
mensuráveis e
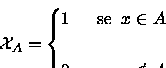
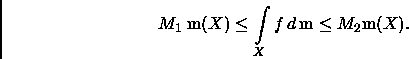
![\begin{proof}% latex2html id marker 1448
[Prova] Seja $X_0\subset X$\space com $...
...\int\limits_{X}\,f_n\,d\ensuremath{\mathfrak{m} }} .\end{displaymath}\end{proof}](img304.gif)
![\begin{proof}% latex2html id marker 1567
[Prova] Seja
\begin{displaymath}F_n=\i...
... {\int\limits_{X}\,f_n\,d\ensuremath{\mathfrak{m} }}\end{displaymath}\end{proof}](img306.gif)
![]() definidas por
definidas por
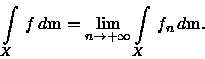
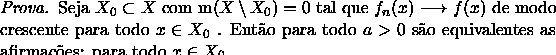
 .
Neste caso
.
Neste caso
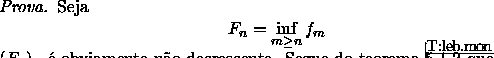
![\begin{proof}[Prova]Para cada $n$\space e $k=1,2\ldots,n2^n$\space seja
\begin{d...
...\end{displaymath}Finalmente $f_n$\space \'e simples para cada $n$ .
\end{proof}](img317.gif)
![]() é integrável
então
é integrável
então
 e
e
![\begin{proof}% latex2html id marker 1734
[Prova]Como $\ensuremath{ \left\vert f\...
...its_{X_0}\,f_n\,d\ensuremath{\mathfrak{m} }}\end{displaymath}\begin
\end{proof}](img327.gif)