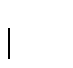 a família das coberturas
enumeráveis de Apor bolas de X B, tais que diam
a família das coberturas
enumeráveis de Apor bolas de X B, tais que diam
É fácil ver que hs é uma medida exterior métrica isto é que
satisfaz:
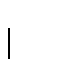 .
Como as s-meddidas de Hausdorff são
importantes exemplos daremos as provas de suas propriedades elementares a
seguir. O lema que segue resume estas propriedades:
.
Como as s-meddidas de Hausdorff são
importantes exemplos daremos as provas de suas propriedades elementares a
seguir. O lema que segue resume estas propriedades:
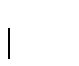 ,
então
,
então
 para todo
t<d denomina-se dimensão de Hausdorff de X e denota-se
para todo
t<d denomina-se dimensão de Hausdorff de X e denota-se
 um
homeomorfismo Lipschitziano isto é, existe c>0 tal que
um
homeomorfismo Lipschitziano isto é, existe c>0 tal que
 então,
então,