Kullback and Leibler's (1951) [65] measure of information associated with the probability distributions
Kullback and Leibler's (1951) [65]
measure of information associated with the probability distributions ![]() and
and ![]() is given by
is given by
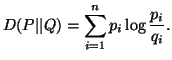 |
(2.1) |
The measure (2.1) has many names given by different authors such as, relative information, directed divergence, cross entropy, function of discrimination etc.. Here we shall refer it "relative information". It has found many applications in setting important theorems in information theory and statistics.
The Kerridge's (1961) [63] measure of information generally referred as inaccuracy associated with two probability distributions is given by
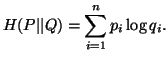 |
(2.2) |
Various authors studied characterizations and properties of the measures (2.1) and (2.2) separately. Here we present their joint study.
Let us consider a measure
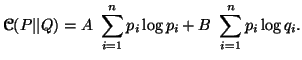 |
(2.3) |
Then for ![]() ,
, ![]() ,
we get (2.1) and for
,
we get (2.1) and for ![]() ,
, ![]() ,
we get (2.2).
,
we get (2.2).
For simplicity, let define
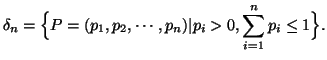
Theorem 2.1. Let ![]() (reals) be a function satisfying the following axioms:
(reals) be a function satisfying the following axioms:
Then ![]() is given by (2.3).
is given by (2.3).
By considering ![]() and
and ![]() in (2.3) we get (2.1). Again taking
in (2.3) we get (2.1). Again taking ![]() and
and ![]() we get (2.2).
we get (2.2).
Measure (2.3) can also be characterized by different approaches using functional equation or axiomatic aprroach. In functional's equation approach, the following two equations are frequently used:
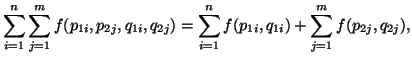
For more details refer to Mathai and Rathai (1975) [71],
Autar (1975) [7], Taneja (1979) [99]
etc..