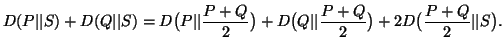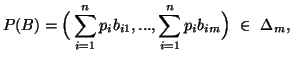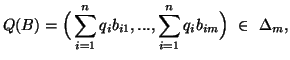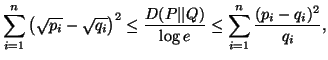Some properties of the measures (2.1) and (2.2) are presented in this subsection. For simplicity, let us denote
Some properties of the measures (2.1) and (2.2) are presented in
this subsection. For simplicity, let us denote![]() and
and![]() .
.
Property 2.1. (Continuity).![]()
![]() and
and![]() are continuous functions of the pair
are continuous functions of the pair ![]() .
.
Property 2.2. (Symmetry).![]() and
and![]() are symmetric functions of their arguments in pair
are symmetric functions of their arguments in pair ![]() ,
i.e., for
,
i.e., for![]() and 2, we have
and 2, we have
Property 2.3. (Expansibility). For![]() and 2, we have
and 2, we have
![]()
Property 2.4. (Additivity). For ![]() and 2, we have
and 2, we have
![]()
Property 2.5. (Sum representation). We can write
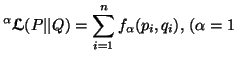 and
andProperty 2.6. (Nonnegativity).![]() and
and![]() ,
with equality iff
,
with equality iff ![]() for
for ![]() and
and![]()
![]() for
for ![]() .
.
Property 2.7. (Recursivity). For![]() and
and ![]() ,
we have
,
we have
![]()
Property 2.8. (Strongly additive). For![]() =
=![]() ,
, ![]()
![]() ,
,![]() ,
, ![]() ,
we have
,
we have
![]()
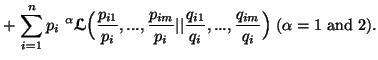
Property 2.9. (Functional equation). Let
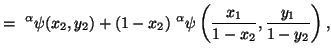
Property 2.10. (Parallelogram identity). For any ![]() ,
,![]() ,
,![]()
![]() ,
we have
,
we have