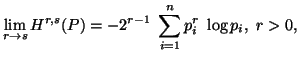![$\displaystyle H^s(P)=(2^{1-s}-1)^{-1}\bigg[\sum_{i=1}^n{p^s_i}-1\bigg],\ s\neq1,\ s>0,$](img627.gif) |
(3.3) |
![$\displaystyle H^s(P)=(2^{1-s}-1)^{-1}\bigg[\sum_{i=1}^n{p^s_i}-1\bigg],\ s\neq1,\ s>0,$](img627.gif) |
(3.3) |
for all ![]() .
In these case also, we can easily verify that
.
In these case also, we can easily verify that ![]() .
.
This quantity permits a simpler characterization (ref. Havrda and Charvát, 1967) [46]. Daróczy (1970) [33] gave an alternative approach to characterize it (see section 3.5.1).
Sharma and Taneja (1975; 1977) [92], [93]
studied a generalization of ![]() involving two scalar parameters, known entropy of degree
involving two scalar parameters, known entropy of degree ![]() ,
and is given by
,
and is given by
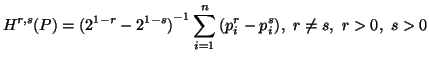 |
(3.4) |
for all ![]() ,
where
,
where ![]() and
and ![]() are real parameters.
are real parameters.
In particular, when ![]() or
or ![]() ,
the measure (3.4) reduces to (3.3). In the limiting case, we have
,
the measure (3.4) reduces to (3.3). In the limiting case, we have