Next:Entropies
of Order andUp:Generalized
Entropy Measures
Previous:Entropy
of Degree and Go to:Table
of Contents
Entropy of kind t
Arimoto (1971) [3] considered generalized 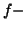 entropies
involving a real function
entropies
involving a real function 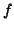 with some conditions (see section 3.5.4). Being an example of these generalized
with some conditions (see section 3.5.4). Being an example of these generalized 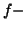 entropies,
Arimoto came up to a generalized entropy involving a real parameter, here
we call it, entropy of kind t, given by
entropies,
Arimoto came up to a generalized entropy involving a real parameter, here
we call it, entropy of kind t, given by
![$\displaystyle _tH(P)={(2^{t-1}-1)}^{-1}\bigg[{\bigg(\sum_{i=1}^n{p^{1/t}_i}\bigg)}^t -1\bigg], \ t\neq 1,\ t>0,$](img633.gif)
|
|
|
(3.5) |
for all 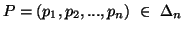 .
In this case also, we can easily verify that
.
In this case also, we can easily verify that 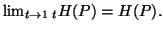
Arimoto's main motivation in considering generalized entropies
was to prove some important results on decision theory connected with bayesian
probability of error.
entropies
was to prove some important results on decision theory connected with bayesian
probability of error.
21-06-2001
Inder Jeet Taneja
Departamento de Matemática - UFSC
88.040-900 Florianópolis, SC - Brazil
![$\displaystyle _tH(P)={(2^{t-1}-1)}^{-1}\bigg[{\bigg(\sum_{i=1}^n{p^{1/t}_i}\bigg)}^t -1\bigg], \ t\neq 1,\ t>0,$](img633.gif)
![$\displaystyle _tH(P)={(2^{t-1}-1)}^{-1}\bigg[{\bigg(\sum_{i=1}^n{p^{1/t}_i}\bigg)}^t -1\bigg], \ t\neq 1,\ t>0,$](img633.gif)
![]() entropies
was to prove some important results on decision theory connected with bayesian
probability of error.
entropies
was to prove some important results on decision theory connected with bayesian
probability of error.