Go to:Table of Contents

Properties of Unified (r,s)-Entropy

This section deals with the properties of unified$(r,s)-$entropy given by (3.8). Unless otherwise specified, from now onwards, it is understood that $P=(p_1,p_2,...,p_n)\ \in\ \Delta_n$, $r,s \in (-\infty,\infty)$. All the logarithms are with base 2.

Property 3.1. (Continuity).${\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P)$ is a continuous function of P.

Property 3.2. (Symmetry).${\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P)$ is a symmetric function of its arguments i.e.,

$${\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(p_1,p_2,...,p_n......emath{\boldsymbol{\mathscr{H}}}}}^s_r(p_{\tau(1)},p_{\tau(2)},...,p_{\tau(n)}),$$ where $\tau$ is any permutation from 1 to n.

Property 3.3. (Normality). We have

$${\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r\big({1\over 2},{1\over 2}\big)=1.$$ Property 3.4. (Nonadditivity). For all$P=(p_1,p_2,...,p_n)\ \in\ \Delta_n$, $Q=(q_1,q_2,...,p_m)\in\Delta_m$, and $P*Q=(p_1q_1,...,p_1q_m,p_2q_1,...,p_2q_m,...,$$p_nq_1,...,p_nq_m)\in \Delta_{nm}$, we have 

$${\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P*Q)={\bf {\ens......bol{\mathscr{H}}}}}^s_r(P){\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(Q).$$

Property 3.5. (Quasilinearity). We can write  $${\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P)=g^{-1}\bigg[......{p_ig\big({\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r\{p_i\}\big)}\bigg],$$ where $${\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(\{p_i\})=\left\......2^{1-s}-1)\big[p^{s-1}_i -1\big], & s\neq 1 \\ -\log p_i\end{array}\right.$$ $0< p_i \leq 1,\ \forall\ i=1,2,...,n$ and $g$ is a strictly monotonic function.

Property 3.6. (Nonnegativity).${\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P)\geq 0$ with equality iff $P=P^0$, where$P^0\in \Delta_n$ is a probability distribution such that one of the probabilities is one and all others are zero i.e.,$P=(0,...,0,1^{i)},0,...,0) \in \Delta_n$.

Property 3.7. (Monotonicity).${\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P)$ is a monotonic decreasing function of $r$ ($s$ fixed).

Property 3.8. (Inequalities among generalized entropies). The following inequalities hold

(i)${\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P)\left\{\begin{array}{ll}......ensuremath{\boldsymbol{\mathscr{H}}}}}^s_1(P), & r\leq 1,\end{array}\right.$

(ii) ${\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P)\left\{\begin{array}{ll}......ensuremath{\boldsymbol{\mathscr{H}}}}}^1_r(P), & s\geq 1,\end{array}\right.$

where $k(s)$ is given by
$k(s) = \left\{\begin{array}{ll} \geq (2^{1-s}-1)^{-1}(1-s)\,ln\,2, & s \neq 1, \\ 1, & s =1\end{array}\right.$

(iii) ${\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P) \left\{\begin{array}{ll}......emath{\boldsymbol{\mathscr{H}}}}}^1_r(P)\geq 1,\ s\geq 1)\end{array}\right.$

Note 3.2. Let us consider the following measure

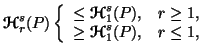
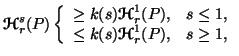
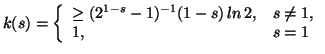
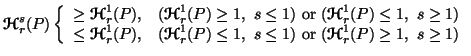
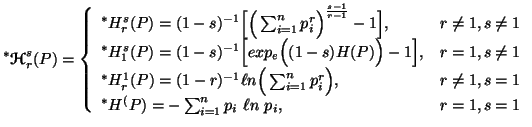$$^*{\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P)=\left\{ \b......\\ ^*H^(P)= -\sum_{i=1}^{n}p_i \,\,\ell n\,\, p_i,&r=1, s=1\end{array}\right.$$ (3.12)

where "$\ell n$" represents the logarithms with natural base "e".

Based on the expression (3.15), the properties 3.7 and 3.8 are extended as follows:

Property 3.7*.$^*{\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P)$ is also a decreasing function of $s$ ($r$ fixed). In particular, when$r=s$, the result still holds.

Property 3.8*. Parts (ii) and (iii) of the property 3.8 are simplified as follows:

$$^*{\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P) \left\{\be......ensuremath{\boldsymbol{\mathscr{H}}}}}^1_r(P), & s\geq 1,\end{array}\right.$$

Property 3.9. (Bounds on ${\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P)$). For $1\leq\sigma \leq n$, the following bounds hold:

(i) ${\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r\Bigg(\sum_{i=1}^{\sigma}p_i,......=1}^\sigma{p_i}\Bigg)\leq {\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P).$

(ii) ${\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P) \leq {\bf {\ensuremath{\b......_{i=1}^\sigma{{p_i\over \sigma}}}_{\sigma -times},p_{\sigma+1},...,p_n\Bigg).$

Property 3.10. (Concavity).${\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P)$ is a concave function of P for all $(r,s)\ \in\ \Gamma$, where

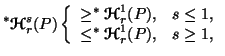
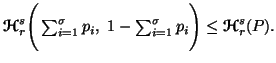
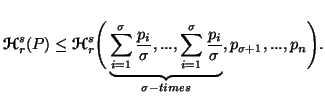
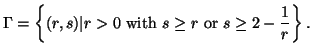$$\Gamma= \left\{ (r,s)\vert r>0\,\, \mbox{with} \,\,s\geq r\,\,\mbox{or} \,\,s\geq 2-{1\over r} \right\} .$$ (3.13)

Note 3.3. The condition $s\geq r> 0$ is better than $s\geq 2-{1\over r}$, $r>0$, but it holds for $s>0$. For $s\leq 0$, we need $2-{1\over r}\leq s\leq 0$. In particular, when $r^{-1}=2-s=t$, the condition $s\geq r> 0$ does not work. In this case, we need the second condition, i.e., $s\geq 2-{1\over r}$, $r>0$. In particular, when $r=s$, $r=1$ or $s=1$ both the conditions, i.e., $s\geq r> 0$ or $s\geq 2-{1\over r}$, $r>0$ works well.

Property 3.11. (Concavity for n=2). For$P\ \in \Delta_2$, ${\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P)$ is concave for all$(r,s) \ \in \ \Gamma \cup\ (1,2]\times (1,\infty)$.

Property 3.12. (Schur-concavity).${\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P)$ is a Schur-concave of $P \in \ \Delta_n$.

Property 3.13. (Maximality).${\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P)$ is maximum for the uniform probability distribution i.e., 

$$0 \leq {\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P) \leq ......suremath{\boldsymbol{\mathscr{H}}}}}^s_r({1\overn},...,{1\over n}),\ n\geq 2.$$ Property 3.14.(Pseudo-concavity).${\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P)$ is a pseudo-concave function of $P$ in $\Delta_n$.

Property 3.15. (Quasiconcavity).${\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P)$ is a quasiconcave function of P in$\Delta_n$.

Property 3.16. (Relative to maximum probability). Let $p_{max}=max\{p_1,p_2,...,p_n\}$, where$P=(p_1,p_2,...,p_n)\ \in\ \Delta_n$, then the followings hold:

(i) ${\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(p_{max},1-p_{max})\leq {\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P)$.

(ii) ${\ensuremath{\boldsymbol{\mathscr{H}}}}^s_r(P) \leq {\bf {\ensuremath{\boldsym......_{max}\over n-1},...,{1-p_{max}\over n-1} }_{(n-1)-\mbox{times}},p_{max}\Big)$.

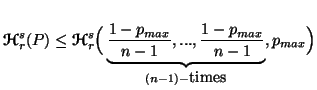(iii) $\lim_{r\to \infty}{ {\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P)}=\l......p^{s-1}_{max}-1],\\ s\neq 1 \\ -\log\, p_{max},\ \ s=1\end{array}\right.$

(iv) $1-p_{max}\leq {1\over 2}{\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P)$, where the part (iv) is true under the following conditions:

($a_1$) $(s\leq 2,\, {1\over n}\leq p_{max} \leq {1\over 2})\$   or$(s\geq 2,\, p_{max} \geq {1\over 2}) \$   for all$\,\,r>0, \$   or$$

($a_2$) $(r,s)\ \in\ \Gamma$   or$(0<r\leq 2,\ s\geq 1)\$   with$\,\, p_{max}\geq {1\over 2}.$

Property 3.17. (Order preserving). For all $P \in \ \Delta_n$, $Q\ \in\ \Delta_m$, we have  $${\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P)>{\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(Q),$$ provided the followings hold:

($a_1$) $H(Q)<-\log{p_{max}}, \,$   and$\,\log{m} < H(P)$ or

($a_2$) for all $r\ \in\ (r_1,r_2)$, where $r_1$ and $r_2$ are such that$H_{r_1}(P)= H(Q)$ and $H_{r_2}(Q)=H(P)$.