Go to:Table of Contents

Unified (r,s)-Entropy for Continuous Probability Distributions

In this section we extend the notion of generalized entropies to the continuous case, and examine some properties of the resulting unified $(r,s)-$entropy function.

Let X be an absolutely continuous random variable, that is, a random variable having a probability density function p(x). The unified $(r,s)-$entropy of X is defined as follows:

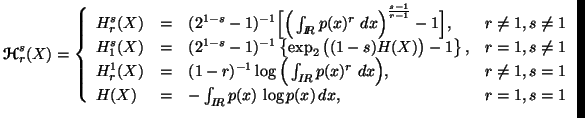$${\ensuremath{\boldsymbol{\mathscr{H}}}}^s_r(X)= \left\{ \begin{ar......(X) & = & -\int_{I\!R}{p(x)\, \log p(x) \, dx}, & r=1, s=1 \end{array} \right.$$ (3.14)

provided the integrals exist, where $p(x)\geq 0$, $\int_{I\!R}{p(x)\ dx}=1$.

The contrast between continuous and discrete distribution is worth emphasising:

(i) The entropy measure of continuous distribution need not exist.

(ii) When it does exist, there is nothing to ensure that is positive because $p(x)$ can exceed unity. We consider the following examples:

Example 3.1. Let $X$ be a random variable with probability density function  $$p(x)= \lambda \,exp(-\lambda x),\ x>0,\\lambda>0.$$ Then $$H^s_r(X)=(2^{1-s}-1)^{-1}\Big[\big({\lambda^{r-1}\overr}\big)^{s-1\over r-1} -1\Big],\ \ r\neq 1,\ s\neq 1$$ with$H^s_r(X)<0$ when $\lambda > {r^{1/(r-1)}\over 2}$. (iii) The unified $(r,s)-$entropy are not limits of the unified$(r,s)-$entropy of the discrete case. This we shall verify in the following example.

Example 3.2. Let $X$ be a discrete random variable taking the values ${1\over n},{2\over n},...,{n\over n}$ with equal probabilities ${1\over n}$. Then

$$H^s_r(X)=(2^{1-s}-1)^{-1}[n^{1-s} -1],\ \ r\neq 1,\ s\neq 1.$$ As $n$ increases, the distribution of $X$ converges to a continuous uniform distribution in (0,1). If $Y^d_{^=}\ U(0,1)$, we have  $$H^s_r(Y)=0,$$ however, $$\lim_{r\to \infty}{H^s_r(X)}=\left\{\begin{array}{ll}+\infty, & s<1 \\ (1-2^{1-s})^{-1}, & s>1\end{array}\right.$$ (iv) The unified $(r,s)-$entropy is not invariant with respect to a change of variables. We illustrate this point with the following example:

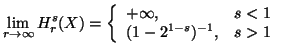
Example 3.3. We consider a function $y=g(x)$, where $g$ is a stricly increasing function of $x$. Since the mapping from $X$ to $Y$ is one to one, we have

$$f_x(x_0)=f_y(y_0)\vert g'(x_0)\vert,$$

where $g(x_0)=y_0$. Therefore, $$H^s_r(Y)=(2^{1-s}-1)^{-1}\Big\{ \Big(\int_{I\! \!R}{f_y(y)^r\,dy}\Big)^{s-1\over r-1}-1 \Big\}$$ $$=(2^{1-s}-1)^{-1}\Big\{\Big(\int_{I\! \!R}{f_x(x)^r\vert g'(x)\vert\, dx}\Big)^{s-1\over r-1}-1\Big\},\ r\neq 1,\ s\neq 1,$$ which is different from $H^s_r(X)$ unless $g$ be the identity function.

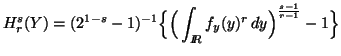
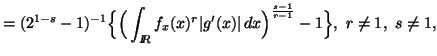
These important differences between discrete and continuous cases are a warning that the results for the discrete distributions cannot be translated to continuous case without independent verification. Fortunately, some of the significant concepts rely upon differences between entropies and for these the difficulties disappear.