Next:Different
Forms of UnifiedUp:Unified
Multivariate Entropies
Previous:Unified
Multivariate Entropies Go to:Table
of Contents
Introduction
The concept of the generalized entropy measures discussed discussed in
Chapter 1 needs to be developed for multivariate probability distributions
- in particular for bivariate cases, especially for problems of communication
that require the analysis of messages sent over a channel and received
at the other end. The same is also required in bounding bayesian probability
of error, comparision of experiments, etc.. Following the notations of
Chapter 1, section 1.4, the joint and individual unified (r,s)-entropies
can be written as 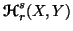 ,
, 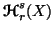 and
and 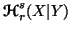 ,
where
,
where 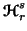 is the unified
is the unified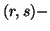 entropy
given by (3.8)
entropy
given by (3.8)
There is no unique way to define the conditional generalized entropy.
It has been defined in different ways by different authors. We shall specify
here four different ways to define the conditional generalized entropy.
We shall observe that these approaches in the limiting case reduce to the
well-known Shannon's conditional entropy given in Chapter 1, section 1.4.
The idea of mutual information has also been generalized for the unified 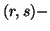 entropy
measures.
entropy
measures.
Henceforth, unless otherwise specified, the letters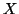 ,
, 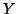 ,
, 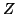 ,
..., etc., will represent discrete, finite random variables.
,
..., etc., will represent discrete, finite random variables.
21-06-2001
Inder Jeet Taneja
Departamento de Matemática - UFSC
88.040-900 Florianópolis, SC - Brazil
![]() entropy
measures.
entropy
measures.
![]() ,
, ![]() ,
, ![]() ,
..., etc., will represent discrete, finite random variables.
,
..., etc., will represent discrete, finite random variables.