Go to:Table of Contents

Different Forms of Unified $(r,s)-$Conditional Entropies

The unified $(r,s)-$conditional entropies for a fixed value of a random variable are given by ${\ensuremath{\boldsymbol{\mathscr{H}}}}^s_r(Y\vert X=x_i)$ for each $i=1,2,...,n$ and ${\ensuremath{\boldsymbol{\mathscr{H}}}}^s_r(X\vert Y=y_i)$ for each $j=1,2,...,m$.

We shall now give four different ways to define unified $(r,s)-$conditional entropies. The first is based on the natural way, as in Shannon's case. The second and third forms are obtained from some of the expressions appearing in between the first form. The fourth is based on the well-known property of Shannon's entropy. These are given by

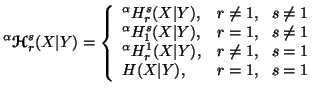$$^\alpha {\ensuremath{\boldsymbol{\mathscr{H}}}}^s_r(X\vert Y)=\le......r(X\vert Y), & r\neq 1,\ \ s=1 \\ H(X\vert Y), &r=1,\ \ s=1\end{array}\right.$$ (6.1)

for all r,s $\in\ (-\infty,\infty)$, $\alpha$=1,2,3 and 4, where for $r\neq 1$, $s\neq 1$, we have

$$^1H^s_r(X\vert Y)=(2^{1-s}-1)^{-1}\sum_{j=1}^m{p(y_j)\Big[\Big(\sum_{i=1}^n{p(x_i\vert y_j)^r}\Big)^\frac{s-1}{r-1}-1\Big]},$$ (6.2)

$$^2H^s_r(X\vert Y)=(2^{1-s}-1)^{-1}\Big[\Big(\sum_{i=1}^n{\sum_{j=1}^m{p(y_j)p(x_i\vert y_j)^r}\Big)^\frac{s-1}{r-1}-1\Big]},$$ (6.3)

$$^3H^s_r(X\vert Y)=(2^{1-s}-1)^{-1}\Big\{\Big[\sum_{j=1}^m{p(y_i)\Big(\sum_{i=1}^n{p(x_i\vert y_j)^r}\Big)^{1/r}\Big]^{r\frac{s-1}{r-1}}-1\Big\}},$$ (6.4)

and

$$^4H^s_r(X\vert Y)=(2^{1-s}-1)^{-1}\Big[\Big(\sum_{i=1}^n{\sum_{j=......g)^{\frac{s-1}{r-1}}-\Big(\sum_{j=1}^m{p(y_j)^r}\Big)^{\frac{s-1}{r-1}}\Big]}.$$ (6.5)

In view of (6.2), we have 

$$^1{\ensuremath{\boldsymbol{\mathscr{H}}}}^s_r(X\vert Y)=\sum_{j=1}^m{p(y_j)}{\ensuremath{\boldsymbol{\mathscr{H}}}}^s_r(X\vert Y=y_j)$$ and in view of (6.5), we have  $$^4{\ensuremath{\boldsymbol{\mathscr{H}}}}^s_r(X\vert Y)={\ensurem......dsymbol{\mathscr{H}}}}^s_r(X,Y)-{\ensuremath{\boldsymbol{\mathscr{H}}}}^s_r(Y).$$

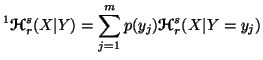
Also, we observe that$^3{\ensuremath{\boldsymbol{\mathscr{H}}}}^s_1(X\vert Y)=\ ^2{\ensuremath{\boldsymbol{\mathscr{H}}}}^s_1(X\vert Y)$, and $^2{\ensuremath{\boldsymbol{\mathscr{H}}}}^s_s(X\vert Y)=\ ^1{\ensuremath{\boldsymbol{\mathscr{H}}}}^s_s(X\vert Y)$. For$r^{-1} = 2-s$, we have $^3{\ensuremath{\boldsymbol{\mathscr{H}}}}^s_r(X\vert Y)=\ ^1{\ensuremath{\boldsymbol{\mathscr{H}}}}^s_r(X\vert Y)$.

In a similar way, we can define the generalized unified $(r,s)-$conditional and joint entropies for three or more random variables $X, Y, Z, ...,$ etc., such as ${\ensuremath{\boldsymbol{\mathscr{H}}}}^s_r(X,Y,Z)$, $^\alpha{\ensuremath{\boldsymbol{\mathscr{H}}}}^s_r(X\vert Y,Z)$, $^\alpha{\ensuremath{\boldsymbol{\mathscr{H}}}}^s_r(X,Y\vert Z)$ ($\alpha =1,2,3$ and $4$), etc..

Note 6.1.$^1H_r^1(X\vert Y)$ is defined in a natural way as of Shannon's entropy. It has been first given by Ben-Bassat and Raviv (1978) [11]. $^2H_r^1(X\vert Y)$ can be seen in Aczél and Daróczy (1963) [1].$^3H_r^1(X\vert Y)$ has been taken by Arimoto (1975) [4]. $^4H_s^s(X\vert Y)$ has been first considered by Daróczy (1970) [33]. Sharma and Mittal (1975) [90] discussed the cases $^2H_r^s(X\vert Y)$ and $^2H_1^s(X\vert Y)$. While we have considered here the much more general and unified way of each of these generalized conditional entropies

In this chapter, we shall study some properties of the generalized conditional entropies defined above. For proof refer to Rathie and Taneja (1991) [81] and Taneja (1988;1995) [104], [108].