Método de Eliminação de Gauss-Jordan

A seguir daremos exemplos de resolução de sistemas utilizando as operações elementares sobre linhas, ou seja, usando escalonamento.

Exemplo 4. Resolver o sistema

$$\left\{ {{\begin{array}{*{20}c} {x + 2y - 3z} & { = 5} \\ ... ... - 2} \\ {x - 3y + 5z} & { = - 1} \\ \end{array} }} \right.$$

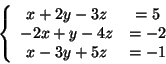
Resolução. Veja os comandos a seguir:

$>$ sys_4:={x+2*y-3*z=5,-2*x+y-4*z=-2,x-3*y+5*z=-1};

$$sys\_4: = \{ - 2x + y - 4z = - 2,x - 3y + 5z = - 1,x + 2y - 3z = 5\}$$

$>$ A:=genmatrix(sys_4,{x,y,z},B);

$$A: = \left[ {{\begin{array}{*{20}c} { - 2} \hfill & 1 \hfil... ...1 \hfill & 2 \hfill & { - 3} \hfill \\ \end{array} }} \right]$$

$>$ det(A);evalm(B);

$$- 10$$

$$[ - 2, - 1,5]$$

$>$ A_B:=augment(A,B);

$$A\_B: = \left[ {{\begin{array}{*{20}c} { - 2} \hfill & 1 \h... ...2 \hfill & { - 3} \hfill & 5 \hfill \\ \end{array} }} \right]$$

$>$ A_B_1:=addrow(A_B,1,2,1/2);

$$A\_B\_1: = \left[ {{\begin{array}{*{20}c} { - 2} \hfill & 1... ...2 \hfill & { - 3} \hfill & 5 \hfill \\ \end{array} }} \right]$$

$>$ A_B_2:=addrow(A_B_1,1,3,1/2);

$$A\_B\_2: = \left[ {{\begin{array}{*{20}c} { - 2} \hfill & 1... ...} \hfill & { - 5} \hfill & 4 \hfill \\ \end{array} }} \right]$$

$>$ A_B_3:=addrow(A_B_2,2,3,1);

$$A\_B\_3: = \left[ {{\begin{array}{*{20}c} { - 2} \hfill & 1... ...0 \hfill & { - 2} \hfill & 2 \hfill \\ \end{array} }} \right]$$

$>$ mulrow(%,1,-1/2):mulrow(%,2,-2/5): A_B_4:=mulrow(%,3, -1/2);

$$A\_B\_4: = \left[ {{\begin{array}{*{20}c} 1 \hfill & {\frac... ...0 \hfill & 1 \hfill & { - 1} \hfill \\ \end{array} }} \right]$$

$>$ A_B_5:=addrow(A_B_4,2,1,1/2);

$$A\_B\_5: = \left[ {{\begin{array}{*{20}c} 1 \hfill & 0 \hfi... ...0 \hfill & 1 \hfill & { - 1} \hfill \\ \end{array} }} \right]$$

$>$ A_B_6:=addrow(A_B_5,3,2,6/5);

$$A\_B\_6: = \left[ {{\begin{array}{*{20}c} 1 \hfill & 0 \hfi... ...0 \hfill & 1 \hfill & { - 1} \hfill \\ \end{array} }} \right]$$

$>$ A_B_7:=addrow(A_B_6,3,1,-7/5);

$$A\_B\_7: = \left[ {{\begin{array}{*{20}c} 1 \hfill & 0 \hfi... ...0 \hfill & 1 \hfill & { - 1} \hfill \\ \end{array} }} \right]$$

$>$ X:=submatrix(A_B_7,1..3,4..4);

$$X: = \left[ {{\begin{array}{*{20}c} {\frac{14}{5}} \hfill \... ... - 2}{5}} \hfill \\ { - 1} \hfill \\ \end{array} }} \right]$$

Logo, concluímos que o sistema tem única solução dada por

$x = \frac{14}{5}, \quad y = \frac{ - 2}{5}$e $z = - 1$.